题目内容

盒子中装有形状、大小完全相同的五张卡片，分别标有数字1，2，3，4，5．现从中任意抽出三张．
（1）求三张卡片所标数字之和能被3整除的概率；
（2）求三张卡片所标数字之积为偶数的条件下，三张卡片数字之和为奇数的概率．
考点：古典概型及其概率计算公式
专题：概率与统计
分析：（1）列举所有满足条件的从中任意抽出三张的基本事件有10个，找到满足标数字之和能被3整除的有4个，根据概率公式计算即可，
（2）根据条件概率公式，计算即可．
解答： 解：（1）事件总体中有10个基本事件：（123）（124）（125）（134）（135）（145）（234）（235）（245）（345），
满足条件的有4个：（123）（135）（234）（345），
故所求概率为P=
4
10
=
2
5
．
（2）设“三张卡片所标数字之积为偶数”为事件M，含9个基本事件（除（135）外），
“三张卡片数字之和为奇数”为事件N，则M•N含3个基本事件（（124）（234）（245）），
故所求条件概率为P(N|M)=
n(M•N)
n(M)
=
3
9
=
1
3
．
点评：本题主要考查了古典概型问题的概率的求法，关键是不重不漏的列举所有满足条件的基本事件．
练习册系列答案
相关题目
下列表示图书借阅的流程正确的是（　　）
A、入库→阅览→借书→找书→出库→还书
B、入库→找书→阅览→借书→出库→还书
C、入库→阅览→借书→找书→还书→出库
D、入库→找书→阅览→借书→还书→出库
判断下列向量
a
与
b
是否共线（其中
e
，
e1
，
e2
是任意向量）：
（1）
a
=3
e
，
b
=-4
e
；
（2）
a
=
0
，
b
=2
e
；
（3）
a
=2
e1
-
e2
，
b
=-4
e1
+2
e2
．
已知函数f（x）=a（x+
1
x
）+2lnx，g（x）=x2．
（Ⅰ）若a＞0且a≠2，直线l与函数f（x）和g（x）的图象切于同一点，求切线l的方程；
（Ⅱ）若?x1[e-1，e]，?x2[-1，2]，使不等式f（x1）＞g（x2）成立，求a的取值范围．
某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x 2 4 5 6 8
y 30 40 60 50 70
（1）求回归直线方程；
（2）试预测广告费支出为10百万元时，销售额多大？
（3）在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．
（b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
xi2-n
.
x
2
，a=
.
y
-b
.
x
）
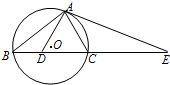已知圆O的内接△ABC中，D为BC上一点，且△ADC为正三角形，点E为BC的延长线上一点，AE为圆O的切线，求证：CD2=BD•EC．
已知f（α）=
sin2(π-α)•cos(2π-α)•tan(-π+α)
sin(-π+α)•tan(-α+3π)
．
（1）化简f（α）；
（2）若α=-
31π
3
，求f（α）的值．
已知f（x）=x-
a
x
（a＞0），g（x）=2lnx+bx，且直线y=2x-2与曲线y=g（x）相切．
（Ⅰ）若对[1，+∞）内的一切实数x，不等式f（x）≥g（x）恒成立，求实数a的取值范围；
（Ⅱ）（ⅰ）当a=1时，求最大的正整数k，使得任意k个实数x1，x2，…xk∈[e，3]（e=2.71828…是自然对数的底数）都有f（x1）+f（x2）+…+f（xk-1）≤16g（xk）成立；
（ⅱ）求证：
1•4
4•12-1
+
2•4
4•22-1
+…+
n•4
4•n2-1
＞ln（2n+1）．
在△ABC中，BC=3，AB=2，且
sinC
sinB
=
2
5
（
6
+1），则A=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网