题目内容
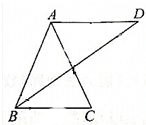
如图，在△ABC中，AB=AC=3，BC=2，∠ABC的平分线交BC的平行线于点D，则△ABD的面积为（ ）
A、3
| ||
B、
| ||
C、3
| ||
| D、6 |
考点：相似三角形的性质
专题：计算题,立体几何
分析：先确定AD，AD上的高，再求△ABD的面积．
解答：
解：∵AB=AC=3，BC=2，∠ABC的平分线交BC的平行线于点D，
∴AD=AB=3，
∵BC上的高为
=2
，
∴AD上的高为2
，
∴△ABD的面积为
×3×2
=3
，
故选：A．
∴AD=AB=3，
∵BC上的高为
| 9-1 |
| 2 |
∴AD上的高为2
| 2 |
∴△ABD的面积为
| 1 |
| 2 |
| 2 |
| 2 |
故选：A．
点评：本题考查角平分线的性质，考查三角形面积的计算，确定AD，AD上的高是关键．
练习册系列答案
相关题目
已知两定点F1（-5，0），F2（5，0），动点P满足|PF1|-|PF2|=2a，当a=3和a=5时，点P的轨迹分别为（ ）
| A、都是双曲线 |
| B、都是射线 |
| C、双曲线的一支和一条射线 |
| D、都是双曲线的一支 |
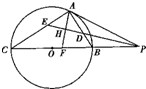如图，直线PA与圆O相切于点A，PBC是过点O的割线，∠APC的角平分线交AC于点E，交AB于点D，点H是线段ED的中点，连接AH并延长PC交于点F．证明：A，E，F，D四点共圆．
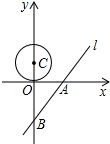如图所示，已知直线l的解析式是y=