题目内容
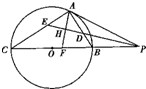 如图,直线PA与圆O相切于点A,PBC是过点O的割线,∠APC的角平分线交AC于点E,交AB于点D,点H是线段ED的中点,连接AH并延长PC交于点F.证明:A,E,F,D四点共圆.
如图,直线PA与圆O相切于点A,PBC是过点O的割线,∠APC的角平分线交AC于点E,交AB于点D,点H是线段ED的中点,连接AH并延长PC交于点F.证明:A,E,F,D四点共圆.考点:与圆有关的比例线段
专题:选作题,立体几何
分析:连接EF,证明EF∥AB,再证明∠AFE=∠ADE,即可证明A,E,F,D四点共圆.
解答:
证明:连接EF,则
∵直线PA与圆O相切于点A,PBC是过点O的割线,∠APC的角平分线交AC于点E,
∴∠PAB=∠PCA,∠APE=∠CPE,
∴∠ADP=∠PEC,△PAC∽△PBA
∴∠AED=∠ADE,
=
∵点H是线段ED的中点,
∴AF平分∠CAB,
∴
=
,
∵∠APC的角平分线交AC于点E,
∴
=
∴
=
,
∴EF∥AB,
∵AB⊥AC,
∴EF⊥AC,
∴∠AEH=∠AFE,
∴∠AFE=∠ADE,
∴A,E,F,D四点共圆.
∵直线PA与圆O相切于点A,PBC是过点O的割线,∠APC的角平分线交AC于点E,
∴∠PAB=∠PCA,∠APE=∠CPE,
∴∠ADP=∠PEC,△PAC∽△PBA
∴∠AED=∠ADE,
| AC |
| AB |
| PC |
| PA |
∵点H是线段ED的中点,
∴AF平分∠CAB,
∴
| CF |
| FB |
| AC |
| AB |
∵∠APC的角平分线交AC于点E,
∴
| CE |
| EA |
| PC |
| PA |
∴
| CE |
| EA |
| CF |
| FB |
∴EF∥AB,
∵AB⊥AC,
∴EF⊥AC,
∴∠AEH=∠AFE,
∴∠AFE=∠ADE,
∴A,E,F,D四点共圆.
点评:本小题主要考查与圆有关的比例线段、四点共圆的证明方法、三角形相似等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
相关题目
已知集合P={x||x-1|≤
,x∈R},Q={x|x∈N},则P∩Q等于( )
| 1 |
| 2 |
| A、[0,1] | B、{0,1} |
| C、{1} | D、{0} |
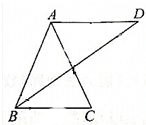
如图,在△ABC中,AB=AC=3,BC=2,∠ABC的平分线交BC的平行线于点D,则△ABD的面积为( )

A、3
| ||
B、
| ||
C、3
| ||
| D、6 |
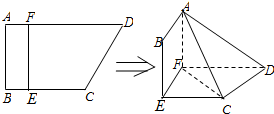 (文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.
(文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.