题目内容
已知椭圆
+
=1的左、右焦点分别为F1、F2,P是椭圆上的一点,且∠F1PF2=60°,则△PF1F2的面积是 .
| x2 |
| 9 |
| y2 |
| 5 |
考点:椭圆的简单性质
专题:计算题,解三角形,圆锥曲线的定义、性质与方程
分析:依题意,在△F1PF2中,∠F1PF2=60°,|F1P|+|PF2|=2a=6,|F1F2|=4,利用余弦定理可求得|F1P|•|PF2|的值,从而可求得△PF1F2的面积.
解答:
解:∵椭圆的方程为
+
=1,
∴a=3,b=
,c=2.
又∵P为椭圆上一点,∠F1PF2=60°,F1、F2为左、右焦点,
∴|F1P|+|PF2|=2a=6,|F1F2|=4,
∴|F1F2|2=(|PF1|+|PF2|)2-2|F1P|•|PF2|-2|F1P|•|PF2|cos60°
=36-3|F1P|•|PF2|=16,
∴|F1P|•|PF2|=
,
∴S△PF1F2=
|F1P|•|PF2|sin60°
=
×
×
=
.
故答案为:
.
| x2 |
| 9 |
| y2 |
| 5 |
∴a=3,b=
| 5 |
又∵P为椭圆上一点,∠F1PF2=60°,F1、F2为左、右焦点,
∴|F1P|+|PF2|=2a=6,|F1F2|=4,
∴|F1F2|2=(|PF1|+|PF2|)2-2|F1P|•|PF2|-2|F1P|•|PF2|cos60°
=36-3|F1P|•|PF2|=16,
∴|F1P|•|PF2|=
| 20 |
| 3 |
∴S△PF1F2=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 20 |
| 3 |
| ||
| 2 |
5
| ||
| 3 |
故答案为:
5
| ||
| 3 |
点评:本题考查椭圆的简单性质,考查余弦定理的应用与三角形的面积公式,属于中档题.

练习册系列答案
相关题目
过抛物线y2=4x的顶点O作互相垂直的两弦OM,ON,则M的横坐标x1与N的横坐标x2之积为( )
| A、64 | B、32 | C、16 | D、4 |
如图,在△ABC中,AB=AC=3,BC=2,∠ABC的平分线交BC的平行线于点D,则△ABD的面积为( )
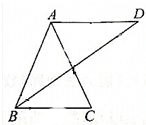

A、3
| ||
B、
| ||
C、3
| ||
| D、6 |
已知数列{an}的前n项和Sn=2n-1,n=1,2,3,…,那么数列{an}( )
| A、是等差数列但不是等比数列 |
| B、是等比数列但不是等差数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列也不是等比数列 |