题目内容
已知直线l:y=kx+b和曲线y=x3-3x+1相切,则斜率k最小时直线l的方程为 .
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,得到导函数的最小值,求出此时x的值,再求出此时的函数值,由直线方程的点斜式求得斜率k最小时直线l的方程.
解答:
解:由y=x3-3x+1,得y′=3x2-3,则y′=3(x2-1)≥-3,
当y′=-3时,x=0,
此时f(0)=1,
∴斜率k最小时直线l的方程为y-1=-3(x-0),即3x+y-1=0.
故答案为:3x+y-1=0.
当y′=-3时,x=0,
此时f(0)=1,
∴斜率k最小时直线l的方程为y-1=-3(x-0),即3x+y-1=0.
故答案为:3x+y-1=0.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点的切线的斜率,就是函数在该点处的导数值,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
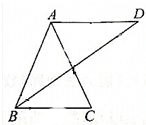
如图,在△ABC中,AB=AC=3,BC=2,∠ABC的平分线交BC的平行线于点D,则△ABD的面积为( )

A、3
| ||
B、
| ||
C、3
| ||
| D、6 |
已知数列{an}的前n项和Sn=2n-1,n=1,2,3,…,那么数列{an}( )
| A、是等差数列但不是等比数列 |
| B、是等比数列但不是等差数列 |
| C、既是等差数列又是等比数列 |
| D、既不是等差数列也不是等比数列 |
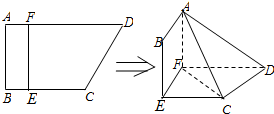 (文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.
(文科做)如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E,F分别在BC,AD上,EF∥AB现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC.