题目内容
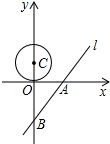 如图所示,已知直线l的解析式是y=
如图所示,已知直线l的解析式是y=| 4 |
| 3 |
考点:圆的切线方程
专题:直线与圆
分析:求出圆和直线相切时的圆心坐标即可得到结论.
解答:
解:设圆和直线相切时的圆心坐标为(0,b),
则直线方程为4x-3y-12=0,
则圆心B到直线的距离d=
=
=
,
即|b+4|=
,解得b=-
=-1.5或b=-
=-6.5
即圆心坐标为(0,-1.5)或(0,-6.5),
则|BC|=1.5-(-1.5)=3或|1.5-(-6.5)|=8,
则运动的时间为3÷1.5=2或8÷1.5=
.
则直线方程为4x-3y-12=0,
则圆心B到直线的距离d=
| |-3b-12| | ||
|
| |3b+12| |
| 5 |
| 3 |
| 2 |
即|b+4|=
| 5 |
| 2 |
| 3 |
| 2 |
| 13 |
| 2 |
即圆心坐标为(0,-1.5)或(0,-6.5),
则|BC|=1.5-(-1.5)=3或|1.5-(-6.5)|=8,
则运动的时间为3÷1.5=2或8÷1.5=
| 16 |
| 3 |
点评:本题主要考查直线和圆的相切的应用,根据条件转化为圆心到直线的距离是解决本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
如图,在△ABC中,AB=AC=3,BC=2,∠ABC的平分线交BC的平行线于点D,则△ABD的面积为( )
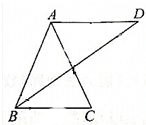

A、3
| ||
B、
| ||
C、3
| ||
| D、6 |