题目内容
已知函数f(x)=2
sinxcosx+2cos2x-1.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)在如图坐标系里用五点法画出函数f(x),x∈[-
,
]的图象.
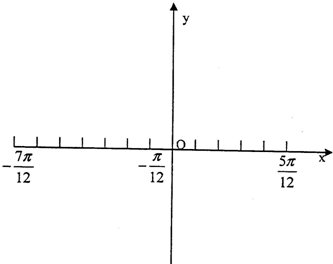
| 3 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)在如图坐标系里用五点法画出函数f(x),x∈[-
| 7π |
| 12 |
| 5π |
| 12 |
| x | -
|
| |||||||

考点:三角函数中的恒等变换应用,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先利用函数关系式的恒等变换,把函数关系式变形成正弦型函数,进一步求出函数的最小正周期.
(2)直接利用(1)的函数关系式利用整体思想求正弦型函数的单调区间.
(3)利用列表,描点.连线求出函数的图象.
(2)直接利用(1)的函数关系式利用整体思想求正弦型函数的单调区间.
(3)利用列表,描点.连线求出函数的图象.
解答:
解:(1)f(x)=2
sinxcosx+2cos2x-1
=2sin(2x+
)
所以:T=
=π
(2)令:
+2kπ≤2x+
≤2kπ+
(k∈Z)
解得:
+kπ≤x≤kπ+
(k∈Z)
所以:函数的单调递减区间为:[
+kπ,kπ+
](k∈Z)
(3)列表:
描点并连线
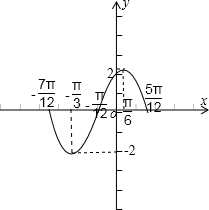
| 3 |
=2sin(2x+
| π |
| 6 |
所以:T=
| 2π |
| 2 |
(2)令:
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得:
| π |
| 6 |
| 2π |
| 3 |
所以:函数的单调递减区间为:[
| π |
| 6 |
| 2π |
| 3 |
(3)列表:
描点并连线
| x | -
| -
| -
|
|
| ||||||||||
2x+
| -π | -
| 0 |
| π | ||||||||||
sin(2x+
| 0 | -1 | 0 | 1 | 0 | ||||||||||
2sin(2x+
| 0 | -2 | 0 | 2 | 0 |

点评:本题考查的知识要点:函数关系似的恒等变换,正弦型函数的周期和单调区间的应用,利用五点法画出函数的图象.属于基础题型.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中,线段BB1与线段AD1所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从高h米的小岛看正东方向有一只船俯角为30°,看正南方向有一只船俯角为45°,则此时两船间的距离为( )
| A、2h米 | ||
B、
| ||
C、
| ||
D、2
|
已知双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
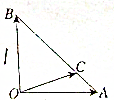 如图所示,在等腰Rt△AOB中,OA=OB=1,
如图所示,在等腰Rt△AOB中,OA=OB=1,