题目内容
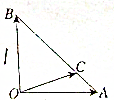如图所示，在等腰Rt△AOB中，OA=OB=1，| AB |
| AC |
| OC |
| OB |
| OA |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：把
用基底
，
表示，然后利用数量积运算展开，代入|
|=|
|=1得答案．
| OC |
| OA |
| OB |
| OA |
| OB |
解答：
解：
=
+
=
+
=
+
(
-
)=
+
，
则
•（
-
）=(
+
)(
-
)=
|
|2-
•
+
•
-
|
|2
=
-
=-
．
故答案为：-
．
| OC |
| OA |
| AC |
| OA |
| 1 |
| 4 |
| AB |
| OA |
| 1 |
| 4 |
| OB |
| OA |
| 1 |
| 4 |
| OB |
| 3 |
| 4 |
| OA |
则
| OC |
| OB |
| OA |
| 1 |
| 4 |
| OB |
| 3 |
| 4 |
| OA |
| OB |
| OA |
| 1 |
| 4 |
| OB |
| 1 |
| 4 |
| OB |
| OA |
| 3 |
| 4 |
| OA |
| OB |
| 3 |
| 4 |
| OA |
=
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
点评：本题考查了平面向量的数量积运算，关键是把
用基底
，
表示，是基础题．
| OC |
| OA |
| OB |
练习册系列答案
相关题目
数列{an}满足a1=
，
=
-1（n∈N*），则a10=（ ）
| 1 |
| 2 |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，则cos∠DAC=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|