复数z=$\frac{i}{2-i}$在复平面内对应的点在( )A．第一象限B．第二象限C．第三象限D．第四象限题目和参考答案——青夏教育精英家教网—

题目内容

12．复数z=$\frac{i}{2-i}$（i是虚数单位）在复平面内对应的点在（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

分析由复数代数形式的乘除运算化简复数z，求出z在复平面内对应的点的坐标，则答案可求．

解答解：z=$\frac{i}{2-i}$=$\frac{i（2+i）}{（2-i）（2+i）}=\frac{-1+2i}{5}=-\frac{1}{5}+\frac{2}{5}i$，
则复数z=$\frac{i}{2-i}$（i是虚数单位）在复平面内对应的点的坐标为：（$-\frac{1}{5}$，$\frac{2}{5}$），位于第二象限．
故选：B．

点评本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案

3．若复数z=log₂（x²-3x-3）+ilog₂（x-3）为实数，则x的值为4．

20．复数$\frac{2i}{1+i}（i$为虚数单位）实部与虚部的和为（　　）

7．若集合A={x|y=${x^{\frac{1}{2}}$}，B={x|y=ln（x+1）}，则A∩B=（　　）

17．设f（x）=$\left\{\begin{array}{l}{\sqrt{x}，0＜x＜1}\\{2（x-1），x≥1}\end{array}\right.$若f（a）=f（a+1），则f（$\frac{1}{a}$）=（　　）

4．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，则|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是4，最大值是$2\sqrt{5}$．

1．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．

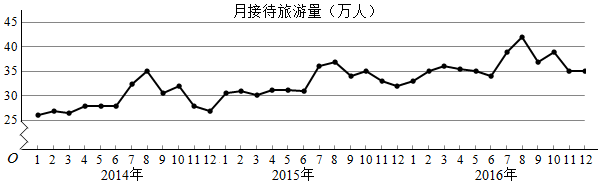
根据该折线图，下列结论错误的是（　　）

	A．	月接待游客量逐月增加
	B．	年接待游客量逐年增加
	C．	各年的月接待游客量高峰期大致在7，8月
	D．	各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

2．函数f（x）在（-∞，+∞）单调递减，且为奇函数．若f（1）=-1，则满足-1≤f（x-2）≤1的x的取值范围是（　　）

试题分类