题目内容
4.已知向量$\overrightarrow{a}$、$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是4,最大值是$2\sqrt{5}$.分析 通过记∠AOB=α(0≤α≤π),利用余弦定理可可知|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5+4cosα}$、|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5-4cosα}$,进而换元,转化为线性规划问题,计算即得结论.
解答 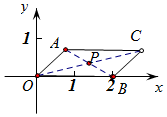 解:记∠AOB=α,则0≤α≤π,如图,
解:记∠AOB=α,则0≤α≤π,如图,
由余弦定理可得:
|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{5+4cosα}$,
|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{5-4cosα}$,
令x=$\sqrt{5-4cosα}$,y=$\sqrt{5+4cosα}$,
则x2+y2=10(x、y≥1),其图象为一段圆弧MN,如图,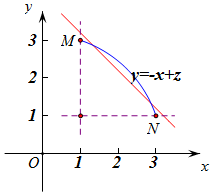
令z=x+y,则y=-x+z,
则直线y=-x+z过M、N时z最小为zmin=1+3=3+1=4,
当直线y=-x+z与圆弧MN相切时z最大,
由平面几何知识易知zmax即为原点到切线的距离的$\sqrt{2}$倍,
也就是圆弧MN所在圆的半径的$\sqrt{2}$倍,
所以zmax=$\sqrt{2}$×$\sqrt{10}$=$2\sqrt{5}$.
综上所述,|$\overrightarrow{a}$+$\overrightarrow{b}$|+|$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是4,最大值是$2\sqrt{5}$.
故答案为:4、$2\sqrt{5}$.
点评 本题考查函数的最值及其几何意义,考查数形结合能力,考查运算求解能力,涉及余弦定理、线性规划等基础知识,注意解题方法的积累,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
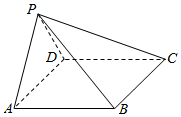 如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.