题目内容
7.若集合A={x|y=${x^{\frac{1}{2}}$},B={x|y=ln(x+1)},则A∩B=( )| A. | [0,+∞) | B. | (0,1) | C. | (-1,+∞) | D. | (-∞,-1) |
分析 分别根据根式的被开放式非负,对数的真数大于0,化简集合A,B,再由交集的定义,即可得到所求集合.
解答 解:集合A={x|y=${x^{\frac{1}{2}}$}={x|x≥0}
B={x|y=ln(x+1)}={x|x+1>0}={x|x>-1},
则A∩B={x|x≥0}=[0,+∞).
故选:A.
点评 本题考查集合的交集运算,同时考查函数的定义域的求法,运用定义法解题是关键,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
18.已知函数f(x)=3x-($\frac{1}{3}$)x,则f(x)( )
| A. | 是奇函数,且在R上是增函数 | B. | 是偶函数,且在R上是增函数 | ||
| C. | 是奇函数,且在R上是减函数 | D. | 是偶函数,且在R上是减函数 |
2.已知复数$z=\frac{{a+{i}}}{{1+{i}}}$(a∈R)的实部为2,则$\overline z$=( )
| A. | 2+i | B. | 2-i | C. | $2-\frac{1}{2}{i}$ | D. | $2+\frac{1}{2}{i}$ |
12.复数z=$\frac{i}{2-i}$(i是虚数单位)在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |




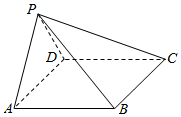 如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.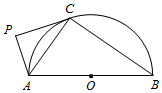 如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.