题目内容
2．函数f（x）在（-∞，+∞）单调递减，且为奇函数．若f（1）=-1，则满足-1≤f（x-2）≤1的x的取值范围是（ ）| A． | [-2，2] | B． | [-1，1] | C． | [0，4] | D． | [1，3] |
分析 由已知中函数的单调性及奇偶性，可将不等式-1≤f（x-2）≤1化为-1≤x-2≤1，解得答案．
解答 解：∵函数f（x）为奇函数．
若f（1）=-1，则f（-1）=1，
又∵函数f（x）在（-∞，+∞）单调递减，-1≤f（x-2）≤1，
∴f（1）≤f（x-2）≤f（-1），
∴-1≤x-2≤1，
解得：x∈[1，3]，
故选：D
点评 本题考查的知识点是抽象函数及其应用，函数的单调性，函数的奇偶性，难度中档．
练习册系列答案
相关题目
12．复数z=$\frac{i}{2-i}$（i是虚数单位）在复平面内对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
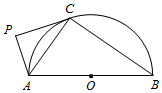如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．