题目内容
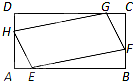如图，已知矩形ABCD，AB=2，AD=1．若点E，F，G，H分别在线段AB，BC，CD，DA上，且AE=BF=CG=DH，则四边形EFGH面积的最小值为考点：三角形的面积公式,三角函数的最值
专题：解三角形
分析：设出AE，则AH，CF，DG，BE可分别表示，进而利用矩形减去四个三角形的面积即可得到所求面积的表达式，利用二次函数的性质求得最小值．
解答：
解：设AE=x，则AH=CF=1-x，DG=BE=2-x，
∴四边形EFGH面积为S矩形ABCD-2（S△AEH+S△BEF）=2-2[x•（1-x）+x（2-x）]=2x2-3x+2，（0＜x＜2）
对称轴为x=
，开口方向向上，
∴当x=
时，四边形的面积取到最小值最小值为：2×
-3×
+2=
，
故答案为：
．
∴四边形EFGH面积为S矩形ABCD-2（S△AEH+S△BEF）=2-2[x•（1-x）+x（2-x）]=2x2-3x+2，（0＜x＜2）
对称轴为x=
| 3 |
| 4 |
∴当x=
| 3 |
| 4 |
| 9 |
| 16 |
| 3 |
| 4 |
| 7 |
| 8 |
故答案为：
| 7 |
| 8 |
点评：本题主要考查了二次函数的性质．解题的关键是建立数学模型，把问题转化为二次函数来解决．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
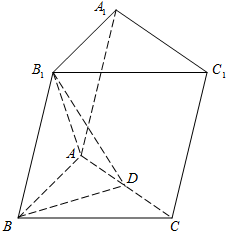如图，在三棱柱ABC-A1B1C1中，B1B=B1A=AB=BC=2，∠B1BC=90°，D为AC的中点，AB⊥B1D．
如图正方体ABCD-A1B1C1D1，下面结论正确的是已知数列{an}的通项公式是an=n2sin（
π），则a1+a2+a3+…+a2014=（ ）
| 2n+1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|