题目内容
在某批次的某种灯泡中,随机地抽取200个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(Ⅰ)根据频率分布表中的数据,写出a,b的值;
(Ⅱ)某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求n的最小值;
(Ⅲ)某人从这个批次的灯泡中随机地购买了3个进行使用,若以上述频率作为概率,用X表示此人所购买的灯泡中次品的个数,求X的分布列和数学期望.
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | a |
| [300,400) | 70 | 0.35 |
| [400,500) | b | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
(Ⅱ)某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求n的最小值;
(Ⅲ)某人从这个批次的灯泡中随机地购买了3个进行使用,若以上述频率作为概率,用X表示此人所购买的灯泡中次品的个数,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,分层抽样方法
专题:概率与统计
分析:(Ⅰ)利用频率分布表中的数据直接计算能求出a、b的值.
(Ⅱ)由频率分布表知按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*)个,由此能求出n的最小值.
(Ⅲ)X的所有取值为0,1,2,3.分别求出相对应的概率,由此能求出X的分布列和数学期望.
(Ⅱ)由频率分布表知按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*)个,由此能求出n的最小值.
(Ⅲ)X的所有取值为0,1,2,3.分别求出相对应的概率,由此能求出X的分布列和数学期望.
解答:
(本小题满分13分)
解:(Ⅰ)a=1-0.10-0.35-0.15-0.25=0.15,
b=200-20-30-70-50=30.…(2分)
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,
∴优等品、正品和次品的比例为50:100:50=1:2:1.…(4分)
∴按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*),
∴n的最小值为4.…(6分)
(Ⅲ)X的所有取值为0,1,2,3.…(7分)
由题意,购买一个灯泡,且这个灯泡是次品的概率为0.1+0.15=0.25,…(8分)
从本批次灯泡中购买3个,可看成3次独立重复试验,
∴P(X=0)=
×(1-
)3=
,
P(X=1)=
×
×(1-
)2=
,
P(X=2)=
×(
)2(1-
)1=
,
P(X=3)=
×(
)3=
.…(11分)
∴随机变量X的分布列为:
…(12分)
∴X的数学期望E(X)=0×
+1×
+2×
+3×
=
.
…(13分)
(注:写出X~B(3,
),P(X=k)=
(
)k(1-
)3-k,k=0,1,2,3.请酌情给分)
解:(Ⅰ)a=1-0.10-0.35-0.15-0.25=0.15,
b=200-20-30-70-50=30.…(2分)
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,
∴优等品、正品和次品的比例为50:100:50=1:2:1.…(4分)
∴按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*),
∴n的最小值为4.…(6分)
(Ⅲ)X的所有取值为0,1,2,3.…(7分)
由题意,购买一个灯泡,且这个灯泡是次品的概率为0.1+0.15=0.25,…(8分)
从本批次灯泡中购买3个,可看成3次独立重复试验,
∴P(X=0)=
| C | 0 3 |
| 1 |
| 4 |
| 27 |
| 64 |
P(X=1)=
| C | 1 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 27 |
| 64 |
P(X=2)=
| C | 2 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
P(X=3)=
| C | 3 3 |
| 1 |
| 4 |
| 1 |
| 64 |
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
∴X的数学期望E(X)=0×
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
…(13分)
(注:写出X~B(3,
| 1 |
| 4 |
| C | k 3 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
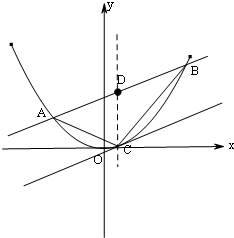 如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).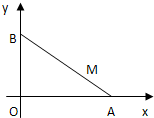 如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上的一点,且
如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上的一点,且 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=