题目内容
求函数y=
的导数.
| x | ||
|
考点:导数的运算
专题:导数的概念及应用
分析:根据复合函数的导数运算法则进行计算,求出正确的答案即可.
解答:
解:∵函数y=
,
∴y′=
=
=
=
=
.
| x | ||
|
∴y′=
x′•
| ||||
(
|
=
| ||||||||
| 1+x2 |
=
| ||||||
| 1+x2 |
=
| (1+x2)-x2 | ||
(1+x2)
|
=
| ||
| (1+x2)2 |
点评:本题考查了求复合函数的导数问题,解题时应按照复合函数的导数运算法则进行计算,即可求出答案.

练习册系列答案
相关题目
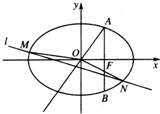 如图,已知椭圆C:
如图,已知椭圆C: