题目内容
4.锐角三角形ABC中.若∠A=2∠B.则$\frac{BC}{AC}$的取值范围为(1,2).分析 由正弦定理可得:$\frac{BC}{AC}$=$\frac{sinA}{sinB}$=2cosB,由于0<A+B<π,可得:0<B<$\frac{π}{3}$,可得$\frac{1}{2}<$cosB<1.即可得出.
解答 解:由正弦定理可得:$\frac{BC}{AC}$=$\frac{a}{b}$=$\frac{sinA}{sinB}$=$\frac{sin2B}{sinB}$=2cosB,
∵0<A+B<π,
∴0<3B<π,
∴0<B<$\frac{π}{3}$,
∴$\frac{1}{2}<$cosB<1.
∴$\frac{BC}{AC}$∈(1,2),
故答案为:(1,2).
点评 本题考查了正弦定理、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
14.12月26号南昌地铁一号线正式运营,从此开创了南昌地铁新时代,南昌人民有了自己开往春天的地铁.设地铁在某段时间内进行调试,由始点起经过t分钟后的距离为s=$\frac{1}{4}$t4-4t3+16t2,则列车瞬时速度为零的时刻是( )
| A. | 4分末 | B. | 8分末 | C. | 0分与8分末 | D. | 0分,4分,8分末 |
16.已知复数z=1+i,则|$\overline{z}$|=( )
| A. | $\sqrt{2}$ | B. | 0 | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
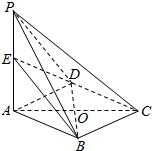 如图,四棱柱P-ABCD中,底面ABCD是菱形,AC∩BD=O,侧棱PA⊥平面ABCD,E是PA的中点.
如图,四棱柱P-ABCD中,底面ABCD是菱形,AC∩BD=O,侧棱PA⊥平面ABCD,E是PA的中点.