题目内容
7.若a≠0,试求函数f(x)=-$\frac{2}{3}$ax3-x2+a2x2+2ax的单调区间与极值.分析 先求出函数的导数,通过讨论a的范围,得到函数的单调区间,从而求出函数的极值即可.
解答 解:∵函数f(x)=-$\frac{2}{3}$ax3-x2+a2x2+2ax,
∴f′(x)=-2ax2-2x+2a2x+2a=(-2ax-2)(x-a),
a>0时,-$\frac{1}{a}$<a,
令f′(x)>0,解得:x>a或x<-$\frac{1}{a}$,
令f′(x)<0,解得:-$\frac{1}{a}$<x<a,
∴f(x)在(-∞,-$\frac{1}{a}$),(a,+∞)递增,在(-$\frac{1}{a}$,a)递减,
∴f(x)极大值=f(-$\frac{1}{a}$)=-$\frac{1}{{3a}^{2}}$-1,f(x)极小值=f(a)=$\frac{1}{3}$a4+a2,
a<0时,-$\frac{1}{a}$>a,
令f′(x)>0,解得:x>-$\frac{1}{a}$或x<a
令f′(x)<0,解得:a<x<-$\frac{1}{a}$,
∴f(x)在(-∞,a),(-$\frac{1}{a}$,+∞)递增,在(a,-$\frac{1}{a}$)递减,
∴f(x)极小值=f(-$\frac{1}{a}$)=-$\frac{1}{{3a}^{2}}$-1,f(x)极大值=f(a)=$\frac{1}{3}$a4+a2.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
16.下列不等式中,正确的是( )
| A. | 0.8-0.1>0.8-0.2 | B. | log0.53>log0.52 | C. | sin$\frac{2π}{5}$<sin$\frac{π}{5}$ | D. | 0.7-0.3>0.82.2 |
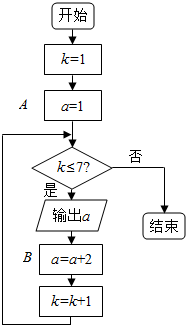 按图所示的程序框图操作:
按图所示的程序框图操作: