题目内容
9.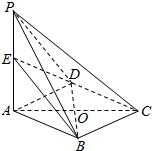 如图,四棱柱P-ABCD中,底面ABCD是菱形,AC∩BD=O,侧棱PA⊥平面ABCD,E是PA的中点.
如图,四棱柱P-ABCD中,底面ABCD是菱形,AC∩BD=O,侧棱PA⊥平面ABCD,E是PA的中点.(1)求证:PC∥平面BED;
(2)求证:PC⊥BD.
分析 (1)由题意易得EO为中位线,EO∥PC,即可得证PC∥平面BED.
(2)由底面ABCD是菱形,可得:BD⊥AC,由侧棱PA⊥平面ABCD,可得:BD⊥PA,从而可证BD⊥平面PAC,即可得证PC⊥BD.
解答 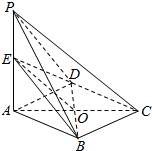 证明:(1)∵底面ABCD是菱形,AC∩BD=O,E是PA的中点.
证明:(1)∵底面ABCD是菱形,AC∩BD=O,E是PA的中点.
∴△PAC中,EO为中位线,EO∥PC,
∵EO?平面BED,PC?平面BED,
∴PC∥平面BED.
(2)∵底面ABCD是菱形,可得:BD⊥AC,
∵侧棱PA⊥平面ABCD,BD?平面ABCD,可得:BD⊥PA,
又∵PA∩AC=A,
∴BD⊥平面PAC,
∵PC?平面PAC,
∴PC⊥BD.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的性质,直线与直线垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
19.设集合A={x|-3≤2x-1≤3},集合B为函数y=lg(x-1)的定义域,则A∪B=( )
| A. | (1,2) | B. | [-1,+∞) | C. | (1,2] | D. | [1,2) |
1.长方体的相邻三个面的面积分别是12,15,20,且它的八个顶点都在同一个球面上,这个球的表面积是( )
| A. | 100π | B. | 60π | C. | 50π | D. | 30π |
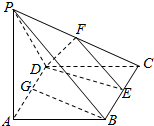 如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,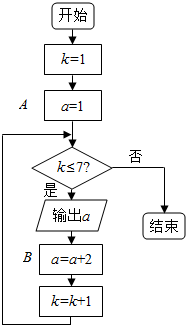 按图所示的程序框图操作:
按图所示的程序框图操作: