题目内容
经过点P(-2,-3),在x轴、y轴上截距相等的直线方程是 .
考点:直线的截距式方程
专题:
分析:分类讨论,当直线过原点,即截距都为零,易得直线方程;当直线不过原点,由截距式,设出直线方程,把P点坐标带入,能求出结果.
解答:
解:当直线过原点,即截距都为零时,
直线经过原点(0,0),P(-2,-3),
直线方程为
=
,
整理,得直线方程为3x-2y=0;
当直线不过原点,由截距式,设直线方程为
+
=1,
把P(-2,-3)代入,得x+y+5=0.
故答案为:x+y+5=0或3x-2y=0
直线经过原点(0,0),P(-2,-3),
直线方程为
| y |
| x |
| -3 |
| -2 |
整理,得直线方程为3x-2y=0;
当直线不过原点,由截距式,设直线方程为
| x |
| a |
| y |
| a |
把P(-2,-3)代入,得x+y+5=0.
故答案为:x+y+5=0或3x-2y=0
点评:本题考查直线方程的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x、y满足约束条件
,则目标函数z=2x+y( )
|
| A、最大值为1 |
| B、最大值为2 |
| C、最大值为3 |
| D、以上都不对 |
cos660°的值为( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
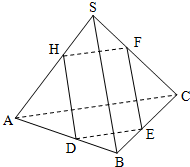 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于