题目内容
某产品广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程
=
x+
中的
为9.4,据此预测广告费用为6万元时销售额为 万元.
| 广告费用x万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | 39 | 49 | 54 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
考点:线性回归方程
专题:应用题,概率与统计
分析:首先求出所给数据的平均数,得到样本中心点,根据线性回归直线过样本中心点,求出方程中的一个系数,得到线性回归方程,把自变量为7代入,预报出结果.
解答:
解:∵
=
(2+3+4+5)=3.5,
=
(26+39+49+54)=42,
∵数据的样本中心点在线性回归直线上,回归方程
=
x+
中的
为9.4,
∴42=9.4×3.5+a,
∴a=9.1,
∴线性回归方程是
=9.4x+9.1,
∴广告费用为6万元时销售额为9.4×6+9.1=65.5万元,
故答案为:65.5.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
∵数据的样本中心点在线性回归直线上,回归方程
 |
| y |
 |
| b |
 |
| a |
 |
| b |
∴42=9.4×3.5+a,
∴a=9.1,
∴线性回归方程是
 |
| y |
∴广告费用为6万元时销售额为9.4×6+9.1=65.5万元,
故答案为:65.5.
点评:本题考查求回归方程,考查利用回归方程进行预测,解题的关键是根据回归方程必过样本中心点,求出回归系数.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设i为虚数单位,则复数
为( )
| 3+4i |
| i3 |
| A、4+3i | B、4-3i |
| C、-4-3i | D、-4+3i |
对于函数f(x)=sin(πx+
),下列命题正确的是( )
| π |
| 2 |
| A、f(x)的周期为π,且在[0,1]上单调递增 |
| B、f(x)的周期为2,且在[0,1]上单调递减 |
| C、f(x)的周期为π,且在[-1,0]上单调递增 |
| D、f(x)的周期为2,且在[-1,0]上单调递减 |
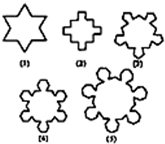 如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则
如图,第一个多边形是由正三角形“扩展”而来,第二个多边形是由正四边形“扩展”而来,…,如此类推,设由正n边形“扩展“而来的多边形的边数记为an.则