题目内容
cos660°的值为（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式中的角度变形后，利用诱导公式及特殊角的三角函数值计算即可得到结果．
解答：
解：cos660°=cos（720°-60°）=cos（-60°）=cos60°=
．
故选：C．
| 1 |
| 2 |
故选：C．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
等比数列{an}的首项a1=-1，a4=27，那么它的前4项之和S4等于（ ）
| A、-34 | B、52 | C、40 | D、20 |
若直线mx+ny+2=0（m＞0，n＞0）截得圆（x+3）2+（y+1）2=1的弦长为2，则
+
的最小值为（ ）
| 1 |
| m |
| 3 |
| n |
| A、6 | B、8 | C、10 | D、12 |
已知
=21，则（2
-
）n的二项展开式中的常数项为（ ）
| C | n-1 n+1 |
| x |
| 1 | ||
|
| A、160 | B、-160 |
| C、960 | D、-960 |
对于函数f（x）=sin（πx+
），下列命题正确的是（ ）
| π |
| 2 |
| A、f（x）的周期为π，且在[0，1]上单调递增 |
| B、f（x）的周期为2，且在[0，1]上单调递减 |
| C、f（x）的周期为π，且在[-1，0]上单调递增 |
| D、f（x）的周期为2，且在[-1，0]上单调递减 |
Sn是数列{an}的前n项和，an=
，则S1=1-
，S2=1-
，S3=1-
，S4=1-
，由此可以归纳出（ ）
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、Sn=1-
| ||
B、Sn=1-
| ||
C、Sn=1-
| ||
D、Sn=1-
|
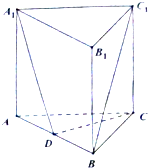如图，在三棱柱ABC-A1B1C1中，AC⊥BC，AB⊥BB1，AC=BC=BB1=2，D为AB的中点，且CD⊥DA1．
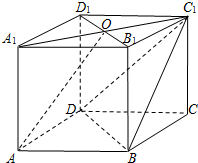在四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，底面ABCD为菱形，O为A1C1