题目内容
已知x、y满足约束条件
，则目标函数z=2x+y（ ）
|
| A、最大值为1 |
| B、最大值为2 |
| C、最大值为3 |
| D、以上都不对 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出可行域，变形目标函数y=-2x+z，平移直线y=-2x，可得结论．
解答：
解：作出
对应的可行域，（如图阴影）
变形目标函数z=2x+y可得y=-2x+z
z为斜率为-2的直线的纵截距，
如图作直线y=-2x，平移该直线，
当平移到经过该阴影部分的A点时，纵截距z最大，
联立
，解得点A（1，0），
∴此时z=2x+y取得最大值是2
故选：B
|
变形目标函数z=2x+y可得y=-2x+z
z为斜率为-2的直线的纵截距，
如图作直线y=-2x，平移该直线，
当平移到经过该阴影部分的A点时，纵截距z最大，
联立
|
∴此时z=2x+y取得最大值是2
故选：B
点评：本题考查简单线性规划，准确作图是解决问题的关键，属基础题．
练习册系列答案
相关题目
已知a＞b＞0，c＞d＞0，下列判断中正确的是（ ）
| A、a-c＜b-d | ||||
| B、ac＞bd | ||||
C、
| ||||
| D、ad＞bc |
设i为虚数单位，则复数
为（ ）
| 3+4i |
| i3 |
| A、4+3i | B、4-3i |
| C、-4-3i | D、-4+3i |
等比数列{an}的首项a1=-1，a4=27，那么它的前4项之和S4等于（ ）
| A、-34 | B、52 | C、40 | D、20 |
若直线mx+ny+2=0（m＞0，n＞0）截得圆（x+3）2+（y+1）2=1的弦长为2，则
+
的最小值为（ ）
| 1 |
| m |
| 3 |
| n |
| A、6 | B、8 | C、10 | D、12 |
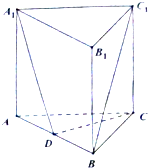如图，在三棱柱ABC-A1B1C1中，AC⊥BC，AB⊥BB1，AC=BC=BB1=2，D为AB的中点，且CD⊥DA1．