题目内容
11.平行四边形ABCD中,AB=2,AD=1,$\overrightarrow{AB}$•$\overrightarrow{AD}$=-1,点M在边CD上,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最大值为( )| A. | 2 | B. | 2$\sqrt{2}$-1 | C. | 5 | D. | $\sqrt{3}$-1 |
分析 先根据向量的数量积的运算,求出A=120°,再建立坐标系,得到$\overrightarrow{MA}$•$\overrightarrow{MB}$=x(x-2)+$\frac{3}{4}$=x2-2x+$\frac{3}{4}$=(x-1)2-$\frac{1}{4}$,设f(x)=(x-1)2-$\frac{1}{4}$,利用函数的单调性求出函数的最值,问题得以解决.
解答  解:∵平行四边形ABCD中,AB=2,AD=1,
解:∵平行四边形ABCD中,AB=2,AD=1,
$\overrightarrow{AB}$•$\overrightarrow{AD}$=-1,点M在边CD上,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|•cos∠A=-1,
∴cosA=-$\frac{1}{2}$,∴A=120°,
以A为原点,以AB所在的直线为x轴,以AB的垂线为y轴,
建立如图所示的坐标系,∴A(0,0),B(2,0),D(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
设M(x,$\frac{\sqrt{3}}{2}$),则-$\frac{1}{2}$≤x≤$\frac{3}{2}$,
∴$\overrightarrow{MA}$=(-x,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{MB}$=(2-x,-$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=x(x-2)+$\frac{3}{4}$=x2-2x+$\frac{3}{4}$=(x-1)2-$\frac{1}{4}$,
设f(x)=(x-1)2-$\frac{1}{4}$,则f(x)在[-$\frac{1}{2}$,1)上单调递减,在[1,$\frac{3}{2}$]上单调递增,
∴f(x)min=f(1)=-$\frac{1}{4}$,f(x)max=f(-$\frac{1}{2}$)=2,
则$\overrightarrow{MA}$•$\overrightarrow{MB}$的最大值是2,
故选:A.
点评 本题考查了向量的数量积定义和向量数量积的坐标表示和函数的最值问题,关键是建立坐标系,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| ξ | -1 | 0 | 1 |
| P | $\frac{1}{3}$ | a | b |
| A. | $\frac{5}{6}$ | B. | $\frac{41}{48}$ | C. | 1 | D. | $\frac{2}{3}$ |
| A. | [-1,3] | B. | (-1,3) | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,-1)∪(3,+∞) |
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| A. | $(-1,-\frac{1}{2})$ | B. | $(1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},1)$ | D. | $(-\frac{1}{2},-1)$ |
| A. | {1} | B. | {0,1} | C. | [0,2) | D. | ∅ |
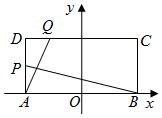 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD上的点,且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$,②直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上.