题目内容
在△ABC中,已知|
|=5,|
|=4,|
|=3,求:
(1)
•
;
(2)
在
方向上的投影;
(3)
在
方向上的投影.
| AB |
| BC |
| AC |
(1)
| AB |
| BC |
(2)
| AC |
| AB |
(3)
| AB |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由三角形的知识易得C=90°,cosA=
,cosB=
,分别由数量积和投影的定义可求.
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:(1)由题意可得|
|2+|
|2=|
|2,
∴C=90°,cosA=
,cosB=
,
∴
•
=5×4×(-
)=-16;
(2)
在
方向上的投影为|
|cosA=3×
=
;
(3)
在
方向上的投影为|
|(-cosB)=-5×
=-4.
| AC |
| BC |
| AB |
∴C=90°,cosA=
| 3 |
| 5 |
| 4 |
| 5 |
∴
| AB |
| BC |
| 4 |
| 5 |
(2)
| AC |
| AB |
| AC |
| 3 |
| 5 |
| 9 |
| 5 |
(3)
| AB |
| BC |
| AB |
| 4 |
| 5 |
点评:本题考查平面向量数量积的运算,涉及向量的投影,属基础题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知椭圆的方程为2x2+3y2=6,则此椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在三棱锥P-ABC中,若PA=PB=PC,则顶点P在底面ABC上的射影O必为△ABC的( )
| A、内心 | B、垂心 | C、重心 | D、外心 |
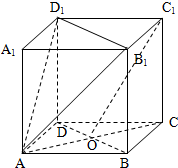 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,