题目内容
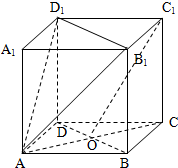 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点,(1)求证:C1O∥面AB1D1;
(2)求二面角A-B1D1-C1的正切值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连接A1C1交B1D1于点O1,连AO1,推出AO1∥C1O,利用在小于平面平行的判定定理证明C1O∥面AB1D1.
(2)连接A1C1交B1D1于点O1,说明∠A1O1A的 补角为二面角A-B1D1-C1的平面角,通过解三角形即可求出所求的二面角的正切值.
(2)连接A1C1交B1D1于点O1,说明∠A1O1A的 补角为二面角A-B1D1-C1的平面角,通过解三角形即可求出所求的二面角的正切值.
解答:
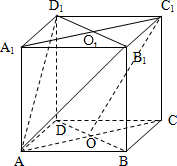 证明:(1)连接A1C1交B1D1于点O1,连AO1,由C1O1∥AO,C1O1=AO,
证明:(1)连接A1C1交B1D1于点O1,连AO1,由C1O1∥AO,C1O1=AO,
知四边形AOC1O1为平行四边形,
得AO1∥C1O. (2分)
又AO1?面AB1D1,C1O?面AB1D1,
故C1O∥面AB1D1. (4分)
(2)解:连接A1C1交B1D1于点O1,显然A1O1⊥D1B1,(5分)
而AA1⊥面A1B1C1D1,B1D1?面A1B1C1D1,
故B1D1⊥面AA1O1,AO1⊥B1D1,
故∠A1O1A的 补角为二面角A-B1D1-C1的平面角. (7分)
AA1=a,则O1A1=
a,
则tan∠AO1A1=
=
,
故所求的二面角的正切值为-
.(8分)
 证明:(1)连接A1C1交B1D1于点O1,连AO1,由C1O1∥AO,C1O1=AO,
证明:(1)连接A1C1交B1D1于点O1,连AO1,由C1O1∥AO,C1O1=AO,知四边形AOC1O1为平行四边形,
得AO1∥C1O. (2分)
又AO1?面AB1D1,C1O?面AB1D1,
故C1O∥面AB1D1. (4分)
(2)解:连接A1C1交B1D1于点O1,显然A1O1⊥D1B1,(5分)
而AA1⊥面A1B1C1D1,B1D1?面A1B1C1D1,
故B1D1⊥面AA1O1,AO1⊥B1D1,
故∠A1O1A的 补角为二面角A-B1D1-C1的平面角. (7分)
AA1=a,则O1A1=
| ||
| 2 |
则tan∠AO1A1=
| AA1 |
| A1O1 |
| 2 |
故所求的二面角的正切值为-
| 2 |
点评:本题考查二面角的平面角的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列三个命题:
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
①一条直线垂直于一个平面内的三条直线,则这条直线和这个平面垂直;
②一条直线与一个平面内的任何直线所成的角相等,则这条直线和这个平面垂直;
③一条直线在平面内的射影是一点,则这条直线和这个平面垂直.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
已知数列{an}满足:a1=1,an+1=2an+3(n∈N*),则a10=( )
| A、210-3 |
| B、211-3 |
| C、212-3 |
| D、213-3 |
下列命题,能得出直线m与平面α平行的是( )
| A、直线m与平面α内 所有直线平行 |
| B、直线m 与平面α内无数条直线平行 |
| C、直线m与平面α没有公共点 |
| D、直线m与平面α内的一条直线平行 |
函数y=2x-5在R上的单调性是( )
| A、增函数 | B、减函数 |
| C、不增不减 | D、无法确定 |