题目内容
4.已知函数f(x)=log2(x2-2ax+3).(1)若a=1,求f(x)的值域;
(2)若a=2,求函数f(x)的定义域及单调区间;
(3)若函数f(x)的定义域为R,求实数a的取值范围;
(4)若函数f(x)的值域为R,求实数a的取值范围;
(5)若函数f(x)在[2,+∞)上单调递增,求实数a的取值范围;
(6)若函数f(x)在[-1,+∞)上有意义,求实数a的取值范围.
分析 (1)求出y=x2-2ax+3的值域,利用对数函数的单调性得出f(x)的值域;
(2)令x2-2ax+3>0解出f(x)的定义域,根据复合函数的单调性得出f(x)的单调性;
(3)令x2-2ax+3>0恒成立解出a的范围;
(4)令y=x2-2ax+3得最小值≤0即可;
(5)根据符合函数的单调性得出y=x2-2ax+3在[2,+∞)上单调递增,且x2-2ax+3>0在[2,+∞)上恒成立,列不等式组解出a的范围;
(6)令x2-2ax+3>0在[-1,+∞)上恒成立,列不等式组解出a的范围
解答 解:(1)a=1时,f(x)=log2(x2-2x+3)=log2[(x-1)2+2],
∵(x-1)2+2≥2,∴f(x)≥log22=1,
∴f(x)的值域为[1,+∞).
(2)当a=2时,f(x)=log2(x2-4x+3),
令x2-4x+3>0得x<1或x>3,
∴f(x)的定义域为(-∞,1)∪(3,+∞).
由二次函数的性质可知y=x2-4x+3在(-∞,1)单调递减,在(3,+∞)单调递增,
∴f(x)=log2(x2-4x+3)在(-∞,1)单调递减,在(3,+∞)单调递增.
(3)若f(x)的定义域为R,则x2-2ax+3>0恒成立,
∴△=4a2-12<0,解得-$\sqrt{3}$<a<$\sqrt{3}$.
(4)设A为y=x2-2ax+3的值域,则A=[3-a2,+∞),
若f(x)的值域为R,则(0,+∞)⊆A,∴3-a2≤0,解得a$≤-\sqrt{3}$或a$≥\sqrt{3}$.
(5)若函数f(x)在[2,+∞)上单调递增,
则y=x2-2ax+3在[2,+∞)上单调递增,且x2-2ax+3>0在[2,+∞)上恒成立,
∴$\left\{\begin{array}{l}{a≤2}\\{7-4a>0}\end{array}\right.$,解得a<$\frac{7}{4}$,
(6)若函数f(x)在[-1,+∞)上有意义,则x2-2ax+3>0在[-1,+∞)上恒成立,
∴$\left\{\begin{array}{l}{a≤-1}\\{4+2a>0}\end{array}\right.$,或△=4a2-12<0,或$\left\{\begin{array}{l}{△=4{a}^{2}-12=0}\\{a<-1}\end{array}\right.$,解得-2<a≤-1或-$\sqrt{3}<a<\sqrt{3}$或a=-$\sqrt{3}$.
综上,a的范围是(-2,$\sqrt{3}$).
点评 本题考查了对数函数的性质,二次函数的性质,符合函数的单调性,属于中档题.

| A. | (-$\frac{π}{6}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | ($\frac{π}{6}$,$\frac{2π}{3}$) | D. | ($\frac{π}{3}$,$\frac{5π}{6}$) |
| 投入促销费用x(万元) | 2 | 3 | 5 | 6 |
| 商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
(2)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(注:$b=\frac{{\sum _{i=1}^n({{x_i}-\bar x})({{y_i}-\bar y})}}{{\sum _{i=1}^n{{({{x_i}-\bar x})}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}},a=\bar y-b•\bar x$)
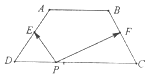 如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )
如图,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分别为AD与BC的中点,对于常数λ,在梯形ABCD的四条边上恰好有8个不同的点P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,则实数λ的取值范围是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |