题目内容
17.设f(x)=$\left\{\begin{array}{l}{1-{x}^{2},x≤1}\\{{x}^{2}+x-2,x>1}\end{array}\right.$,则f[$\frac{1}{f(2)}$]=$\frac{15}{16}$.分析 利用分段函数的解析式,逐步求解函数值即可.
解答 解:f(x)=$\left\{\begin{array}{l}{1-{x}^{2},x≤1}\\{{x}^{2}+x-2,x>1}\end{array}\right.$,
f(2)=22+2-2=4,
$\frac{1}{f(2)}=\frac{1}{4}<1$,
∴f[$\frac{1}{f(2)}$]=f($\frac{1}{4}$)=1-$(\frac{1}{4})^{2}$=$\frac{15}{16}$.
故答案为:$\frac{15}{16}$.
点评 本题考查分段函数的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
12.设A={x|x≥2$\sqrt{2}$},a=3,下列各式正确的是( )
| A. | 0∈A | B. | a∉A | C. | a∈A | D. | {a}∈A |
9.如图是一个几何体的三视图,根据图中数据,该几何体的体积是( )
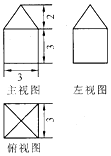

| A. | 27 | B. | 9π | C. | $\frac{27}{4}$π | D. | 33 |
8.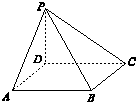 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )| A. | $\frac{1}{3}$(2-$\sqrt{2}$)m | B. | $\frac{1}{2}$(2+$\sqrt{2}$)m | C. | $\frac{1}{2}$(2-$\sqrt{2}$)m | D. | $\frac{1}{6}$(2+$\sqrt{2}$)m |
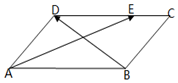 如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.