题目内容
12.设A={x|x≥2$\sqrt{2}$},a=3,下列各式正确的是( )| A. | 0∈A | B. | a∉A | C. | a∈A | D. | {a}∈A |
分析 根据元素与集合的关系进行判断
解答 解:集合A={x|x≥2$\sqrt{2}$},
∵a=3,
3>2$\sqrt{2}$,
∴a∈A,
故选C
点评 本题主要考查元素与集合的关系,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
20.若函数$f(x)=\frac{1}{(2x+1)(x-a)}$为偶函数,则a=( )
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
1.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=m(m≠0)$的渐近线斜率为±2,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{5}$或$\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{3}$或$\frac{{2\sqrt{3}}}{3}$ |
3.当x>1时不等式$\frac{{{x^2}-x+1}}{x-1}≥a$恒成立,则实数a的取值范围是( )
| A. | (-∞,3] | B. | [3,+∞) | C. | (-∞,2] | D. | [2,+∞) |
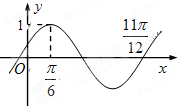 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.