题目内容
8.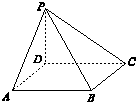 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )| A. | $\frac{1}{3}$(2-$\sqrt{2}$)m | B. | $\frac{1}{2}$(2+$\sqrt{2}$)m | C. | $\frac{1}{2}$(2-$\sqrt{2}$)m | D. | $\frac{1}{6}$(2+$\sqrt{2}$)m |
分析 此球内切于四棱锥时,半径最大,设该四棱锥的内切球的球心为O,半径为r,连接OA,OB,OC,OD,OP,则VP-ABCD=VO-ABCD+VO-PAD+VO-PAB+VO-PBC+VO-PCD,由此能求出此球的最大半径.
解答 解:由题知,此球内切于四棱锥时,半径最大,
设该四棱锥的内切球的球心为O,半径为r,
连接OA,OB,OC,OD,OP,
则VP-ABCD=VO-ABCD+VO-PAD+VO-PAB+VO-PBC+VO-PCD,
即$\frac{1}{3}$×m2×m=$\frac{1}{3}$×m2×r+$\frac{1}{3}$×$\frac{1}{2}$×m2×r+$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{2}$m2×r+$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{2}$m2×r+$\frac{1}{3}$×$\frac{1}{2}$×m2×r,
解得r=$\frac{1}{2}$(2-$\sqrt{2}$)m,
所以此球的最大半径是$\frac{1}{2}$(2-$\sqrt{2}$)m.
故选:C.
点评 本题考查球的最大半径的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
15.已知x5=-243,那么x=( )
| A. | 3 | B. | -3 | C. | -3或3 | D. | 不存在 |
3.当x>1时不等式$\frac{{{x^2}-x+1}}{x-1}≥a$恒成立,则实数a的取值范围是( )
| A. | (-∞,3] | B. | [3,+∞) | C. | (-∞,2] | D. | [2,+∞) |
20.将函数f(x)=cosωx(ω>0)的图象向右平移$\frac{π}{3}$个单位长度后,所得到的图象与原图象关于y轴对称,则ω的最小值为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 6 | D. | 9 |
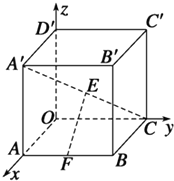 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.