题目内容
8.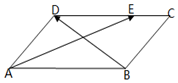 如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
如图,在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,若$\overrightarrow{DE}=2\overrightarrow{EC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.
分析 根据数量积的定义计算出$\overrightarrow{AD}$•$\overrightarrow{AB}$的值,再根据$\overrightarrow{DE}=2\overrightarrow{EC}$用$\overrightarrow{AD}$、$\overrightarrow{AB}$表示出$\overrightarrow{AE}$与$\overrightarrow{BD}$,求出$\overrightarrow{AE}•\overrightarrow{BD}$即可.
解答 解:平行四边形ABCD中,AB=2,AD=1,∠BAD=60°,
∴$\overrightarrow{AD}$•$\overrightarrow{AB}$=1×2×cos60°=1,
又$\overrightarrow{DE}=2\overrightarrow{EC}$,∴$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{DC}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{DC}$=$\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{AB}$,
$\overrightarrow{BD}$=$\overrightarrow{AD}$-$\overrightarrow{AB}$,
∴$\overrightarrow{AE}•\overrightarrow{BD}$=($\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{AB}$)•($\overrightarrow{AD}$-$\overrightarrow{AB}$)=${\overrightarrow{AD}}^{2}$-$\frac{1}{3}$$\overrightarrow{AD}$•$\overrightarrow{AB}$-$\frac{2}{3}$${\overrightarrow{AB}}^{2}$=12-$\frac{1}{3}$×1-$\frac{2}{3}$×22=-2.
故答案为:-2.
点评 本题考查了两个向量的数量积的定义以及公式的应用问题,是基础题目.


| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
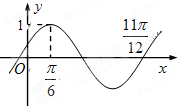 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$|的部分图象如图示,现将函数y=f(x)的图象向右平移$\frac{π}{12}$个单位后,得到函数y=g(x)的图象,则平移后得到的函数解析式g(x)=sin2x.