题目内容

17．设等差数列{an}的前n项和为Sn，a2、a4是方程x2-x-3=0的两个根，S5=$\frac{5}{2}$．

分析 由韦达定理和题可得a2+a4=1，由等差数列的性质整体代入求和公式计算可得．

解答 解：∵等差数列{an}的前n项和为Sn，a2、a4是方程x2-x-3=0的两个根，
∴由韦达定理可得a2+a4=1，∴S5=$\frac{5（{a}_{1}+{a}_{5}）}{2}$=$\frac{5（{a}_{2}+{a}_{4}）}{2}$=$\frac{5}{2}$，
故答案为：$\frac{5}{2}$．

点评 本题考查等差数列的求和公式和性质，整体代换是解决问题的关键，属基础题．

练习册系列答案
相关题目
12．设数列{an}的前n项和为Sn，点（n，$\frac{{S}_{n}}{n}$）（n∈N*）均在函数y=3x-2的图象上．
（1）求证：数列{an}为等差数列；
（2）Tn是数列{$\frac{3}{{{a}_{n}a}_{n+1}}$}的前n项和，求使Tn＜$\frac{m}{20}$对所有n∈N*都成立的最小正整数m．
8．已知命题p：?x0∈R，x0-2＞0，命题q：?x∈R，2x＞x2，则下列命题中为真命题的是（　　）
A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q
5．现有4名选手参加演讲比赛活动，若每位选手可以从4个题目中任意1个，则恰有1个题目没有被这4为选手选中的情况有（　　）
A．36种B．72种C．144种D．288种
12．己知△ABC中，cosB=$\frac{4}{5}$，b=1，sinA=m，若满足条件的三角形只有一个，则m的取值范围是0＜m≤$\frac{3}{5}$，或m=1．
2．已知$f（\frac{2}{x}+1）=lgx$，则f（2）=lg2．
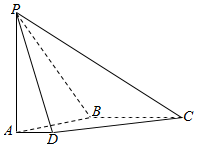9．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AD∥BC，侧棱PA⊥底面ABCD，且PA=AB=BC=2，AD=1．
（Ⅰ）试作出平面PAB与平面PCD的交线EP（不需要说明画法和理由）；
（Ⅱ）求证：直线EP⊥平面PBC．
6．设集合A={x|x2-2x≤0}，B={y|y=x2-2x}，则A∩B=（　　）
A．[-1，2]B．[0，2]C．[-1，+∞）D．[0，+∞）
7．在△ABC中，∠A为钝角，且sinA=$\frac{4}{5}$，c=5，b=4，求a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网