Question

9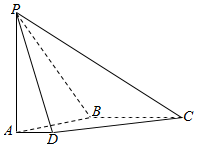．如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AD∥BC，侧棱PA⊥底面ABCD，且PA=AB=BC=2，AD=1．
（Ⅰ）试作出平面PAB与平面PCD的交线EP（不需要说明画法和理由）；
（Ⅱ）求证：直线EP⊥平面PBC．

Answer 1

分析 （Ⅰ）延长BA，CD相交于点E，连接EP，则EP是平面PAB与平面PCD的交线．
（Ⅱ）由已知及平行线的性质可求AB=2，AE=2，利用勾股定理可求$PE=PB=2\sqrt{2}$，而EB=4，可得PE²+PB²=EB²，从而可证EP⊥PB，由PA⊥BC，BC⊥面PAB．可证BC⊥EP，从而可证EP⊥平面PBC．

解答 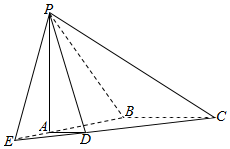（本题满分12分）
解：（Ⅰ）∵底面ABCD是直角梯形，AB⊥AD，AD∥BC，
∴延长BA，CD相交于点E，连接EP，则EP是平面PAB与平面PCD的交线．
平面PAB与平面PCD的交线EP如图所示．
…（4分）
（Ⅱ）∵AD∥BC，BC=2，AD=1，
∴A，D是EB，EC的中点．
∵AB=2，∴AE=2． …（6分）
∵侧棱PA⊥底面ABCD，PA=2，
∴PA⊥AB，
∴$PE=PB=2\sqrt{2}$，而EB=4，
∴PE²+PB²=EB²，∴EP⊥PB． …（8分）
∵侧棱PA⊥底面ABCD，
∴PA⊥BC，
∵AB⊥AD，AD∥BC，
∴BC⊥AB，
∴BC⊥面PAB．
∵EP?面PAB，
∴BC⊥EP． …（10分）
∵BC∩PB=B，
∴EP⊥平面PBC． …（12分）

点评 本题主要考查了直线与平面垂直的判定和性质，考查了勾股定理的应用，考查了空间想象能力和推理论证能力，属于中档题．