题目内容
12.设数列{an}的前n项和为Sn,点(n,$\frac{{S}_{n}}{n}$)(n∈N*)均在函数y=3x-2的图象上.(1)求证:数列{an}为等差数列;
(2)Tn是数列{$\frac{3}{{{a}_{n}a}_{n+1}}$}的前n项和,求使Tn<$\frac{m}{20}$对所有n∈N*都成立的最小正整数m.
分析 (1):将点的坐标代入函数解析式,得到Sn=3n2-2n,再由an=Sn-Sn-1求得an解析式;
(2):写出数列{$\frac{3}{{{a}_{n}a}_{n+1}}$}的通项公式,利用拆项法求得前n项和,根据不等式关系,求得m的值
解答 (1)证明:点(n,$\frac{{S}_{n}}{n}$),(n∈N*)均在函数y=3x-2的图象上.
那么$\frac{{S}_{n}}{n}$=3n-2
∴Sn=3n2-2n
当n=1时,a1=S1=3-2=1
当n≥2时,an=Sn-Sn-1
=3n2-2n-3(n-1)2+2(n-1)
=6n-5;
当n=1时满足,
∴an=6n-5
∴an是以1首项,以6为公比的等差数列an
(2)设${b}_{n}=\frac{3}{{a}_{n}{a}_{n+1}}$
则${b}_{n}=\frac{3}{(6n-5)(6n+1)}$=$\frac{1}{2}(\frac{1}{6n-5}-\frac{1}{6n+1})$
Tn=b1+b2+b3+…+bn
=$\frac{1}{2}(1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+…+\frac{1}{6n-5}-\frac{1}{6n+1})$
=$\frac{1}{2}(1-\frac{1}{6n+1})$
因此使$\frac{1}{2}(1-\frac{1}{6\\;n+1})<\frac{m}{20}$$(\\;n∈N*)$成立的m,必须满足$\frac{1}{2}≤\frac{\\;m}{20}$,
即m≥10,
所以,满足要求的最小正整数m为10.
点评 本题考查了数列与函数的综合应用,用拆项法求数列前n项和以及数列与不等式综合应用问题,属于中档题.

练习册系列答案
相关题目
2.在复平面内,复数z满足z(1-i)=(1+2i)(i是虚数单位),则z对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.方程9x+|3x+b|=5(b∈R)有两个负实数解,则b的取值范囤为( )
| A. | (3,5) | B. | (-5.25,-5) | C. | [-5.25,-5) | D. | 前三个都不正确 |
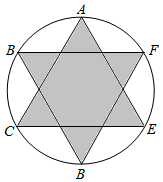 如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.
如图,圆周上的6个点是该圆周的6个等分点,分别连接AC,CE,EA,BD,DF,FB,在圆内部随机投掷一点,则该点不落在阴影部分内的概率是1-$\frac{\sqrt{3}}{π}$.