题目内容
13．设f （x）=$\left\{{\begin{array}{l}{x-3，x≥10}\\{f[f（x+7）]，x＜10}\end{array}}\right.$，则f（6）的值（ ）| A． | 8 | B． | 7 | C． | 6 | D． | 5 |
分析 根据函数的解析式依次求出f（6）的值即可．
解答 解：因为f （x）=$\left\{{\begin{array}{l}{x-3，x≥10}\\{f[f（x+7）]，x＜10}\end{array}}\right.$，
所以f（6）=f[f（13）]=f（10）=10-3=7，
故选B．
点评 本题考查分段函数的函数值，注意自变量的范围，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
4．点M的极坐标（1，π）化成直角坐标为（ ）
| A． | （1，0） | B． | （-1，0） | C． | （0，1） | D． | （0，-1） |
1．不等式$\frac{x-1}{{x}^{2}-4}$＞0的解集为（ ）
| A． | {x|-2＜x＜1} | B． | {x|-2＜x＜1或x＞2} | C． | {x|x＞2} | D． | {x|1＜x＜2或x＜-2} |
5．函数f（x）=2x+x-2的零点所在的区间是（ ）
| A． | （-1，0） | B． | （0，1） | C． | （1，2） | D． | （2，3） |
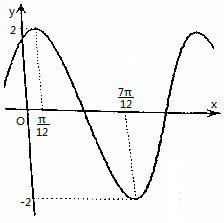已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤π），在一个周期内的图象如图．