题目内容
对于定义在D上的函数y=f(x),若同时满足
(Ⅰ)存在闭区间A=
,B=x,C>0,使得任取x1∈[a,b],都有f(x1)=c(c是常数);
(Ⅱ)对于D内任意x2,当x2∉[a,b]时总有f(x2)>c,则称f(x)为“平底型”函数.
(1)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)若x=4时,f(x)是“平底型”函数,求m和n满足的条件,并说明理由.
(Ⅰ)存在闭区间A=
| π |
| 3 |
(Ⅱ)对于D内任意x2,当x2∉[a,b]时总有f(x2)>c,则称f(x)为“平底型”函数.
(1)判断f1(x)=|x-1|+|x-2|,f2(x)=x-|x-3|是否是“平底型”函数?简要说明理由;
(2)设f(x)是(1)中的“平底型”函数,若|t-1|+|t+1|≥f(x),对一切t∈R恒成立,求实数x的范围;
(3)若x=4时,f(x)是“平底型”函数,求m和n满足的条件,并说明理由.
考点:函数恒成立问题,带绝对值的函数
专题:新定义
分析:(1)考查函数是否全部具备“平底型”函数的定义中的2个条件:①在一个闭区间上,函数值是个常数,
②在闭区间外的定义域内,函数值大于此常数.
(2)要使一个式子大于或等于f(x)恒成立,需使式子的最小值大于或等于f(x)即可,从而得到f(x)≤2,
结合“平底型”函数f(x)的图象可得,当x∈[0.5,2.5]时,f(x)≤2成立.
(3)根据函数解析式,进行分类讨论:m+n>0;m-n≠0;m+n<0;m+n=0;m-n>0;m-n<0;m-n=0,结合图象验证求解.
②在闭区间外的定义域内,函数值大于此常数.
(2)要使一个式子大于或等于f(x)恒成立,需使式子的最小值大于或等于f(x)即可,从而得到f(x)≤2,
结合“平底型”函数f(x)的图象可得,当x∈[0.5,2.5]时,f(x)≤2成立.
(3)根据函数解析式,进行分类讨论:m+n>0;m-n≠0;m+n<0;m+n=0;m-n>0;m-n<0;m-n=0,结合图象验证求解.
解答:
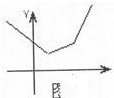 解:(1)f1(x)=|x-1|+|x-2|是“平底型”函数,…1分
解:(1)f1(x)=|x-1|+|x-2|是“平底型”函数,…1分
存在区间[1,2]使得x∈[1,2]时,f(x)=1,当x<1和x>2时,f(x)>1恒成立; …2分
f2(x)=x-|x-3|不是“平底型”函数,…1分
不存在[a,b]⊆D使得任取x∈[a,b],都有f(x)=常数 …1分
(2)若|t-1|+|t+1|≥f(x),对一切t∈R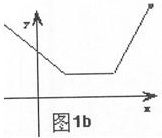
恒成立(|t-1|+|t+1|)min≥f(x)
(|t-1|+|t+1|)min=2 …3分
f(x)≤2即|x-1|+|x-2|≤2
解得
≤x≤
…3分
(3)f(x)=
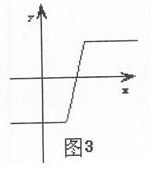
①当m+n>0时若m-n=0时,由图1b知,是“平底型”函数,存在[1,2]使常数 …1分
若m-n≠0时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …1分
②m+n<0不是由图2知,不是“平底型”函数,…1分
③m+n=0
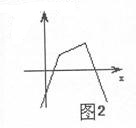
若m-n>0时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件 …1分若m-n<0时,由图4 知不是“平底型”函数,因为不存在区间[a,b]满足条件 …1分若m-n=0时,f(x)=0,显然不是“平底型”函数 …1分
 解:(1)f1(x)=|x-1|+|x-2|是“平底型”函数,…1分
解:(1)f1(x)=|x-1|+|x-2|是“平底型”函数,…1分存在区间[1,2]使得x∈[1,2]时,f(x)=1,当x<1和x>2时,f(x)>1恒成立; …2分
f2(x)=x-|x-3|不是“平底型”函数,…1分
不存在[a,b]⊆D使得任取x∈[a,b],都有f(x)=常数 …1分
(2)若|t-1|+|t+1|≥f(x),对一切t∈R

恒成立(|t-1|+|t+1|)min≥f(x)
(|t-1|+|t+1|)min=2 …3分
f(x)≤2即|x-1|+|x-2|≤2
解得
| 1 |
| 2 |
| 5 |
| 2 |
(3)f(x)=
|


①当m+n>0时若m-n=0时,由图1b知,是“平底型”函数,存在[1,2]使常数 …1分
若m-n≠0时,由图1a知,是“平底型”函数,存在[a,b]满足条件 …1分
②m+n<0不是由图2知,不是“平底型”函数,…1分
③m+n=0
若m-n>0时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件 …1分若m-n<0时,由图4 知不是“平底型”函数,因为不存在区间[a,b]满足条件 …1分若m-n=0时,f(x)=0,显然不是“平底型”函数 …1分
点评:本题的考点是函数恒成立问题,综合考查函数概念及构成要素,及不等式中的恒成立问题,体现等价转化和分类讨论的数学思想,关键是对新概念的理解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知实数k满足
>1.则方程x2-kx+1=0的两个根可分别作为( )
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |
方程组
共有( )组解.
|
| A、1 | B、2 | C、3 | D、4 |
空间四个不同的平面,它们有多种位置关系,从交线数目看,所有可能出现的交线数目的集合是( )
| A、{0,1,2,3,4,5,6} |
| B、{0,1,3,4,5,6} |
| C、{0,1,2,3,5,6} |
| D、{0,1,3,4} |
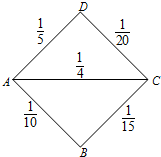 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为