题目内容
若x1和x2(x1<x2)分别是一元二次方程3x2+4x-1=0的两根
求:(1)x1-x2
(2)(x1-2)(x2-2)
求:(1)x1-x2
(2)(x1-2)(x2-2)
考点:一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:利用根与性质之间的关系求两根之和和两根之积的值,然后利用关系式进行转化即可.
解答:
解:∵x1和x2(x1<x2)分别是一元二次方程3x2+4x-1=0的两根,
∴根据根与系数之间的关系可得x1+x2=-
,x1x2=-
.
(1)∵(x1-x2)2=(x1+x2)2-4x1x2,
∴(x1-x2)2=(x1+x2)2-4x1x2=(-
)2-4×(-
)=
,
∵x1<x2,∴x1-x2<0,
即x1-x2=-
=-
.
(2)(x1-2)(x2-2)=x1x2-2(x1+x2)+4=-
-2×(-
)+4=
.
∴根据根与系数之间的关系可得x1+x2=-
| 4 |
| 3 |
| 1 |
| 3 |
(1)∵(x1-x2)2=(x1+x2)2-4x1x2,
∴(x1-x2)2=(x1+x2)2-4x1x2=(-
| 4 |
| 3 |
| 1 |
| 3 |
| 28 |
| 9 |
∵x1<x2,∴x1-x2<0,
即x1-x2=-
|
2
| ||
| 3 |
(2)(x1-2)(x2-2)=x1x2-2(x1+x2)+4=-
| 1 |
| 3 |
| 4 |
| 3 |
| 19 |
| 3 |
点评:本题主要考查一元二次方程根与系数之间的关系的应用,考查学生的转化能力.

练习册系列答案
相关题目
设cos100°=k,则tan80°=( )
A、
| ||||
B、-
| ||||
C、±
| ||||
D、±
|
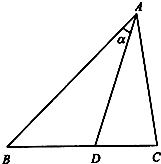 如图,△ABC中,
如图,△ABC中,