Question

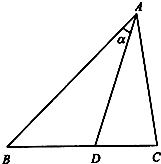如图，△ABC中，B=

π

4

，角A的平分线AD交BC于点D，设∠BAD=α，sinα=

5

5

；
求：
（1）sin∠BAC；
（2）sinC．

Answer 1

考点：三角函数中的恒等变换应用

专题：计算题,三角函数的求值

分析：（1）由∠BAD=α=

1

2

∠BAC＜90°，利用同角三角函数关系算出cosα=

2 5

5

，最后由二倍角的正弦公式可算出sin∠BAC的大小；
（2）由（1）的结论，算出cos∠BAC=cos2α=

3

5

，再由三角形内角和与诱导公式推出sinC=sin（∠BAC+∠B），利用两角和的正弦公式加以计算，可得sinC的值．

解答： 解：（1）∵AD是∠BAC的平分线，∴α=

1

2

∠BAC＜90°，
∵sinα=

5

5

，∴cosα=

1-sin2α

=

2 5

5

由此可得sin∠BAC=sin2α=2sinαcosα=2×

5

5

×

2 5

5

=

4

5

；
（2）由（1）得cos∠BAC=cos2α=1-2sin²α=

3

5

，
∵△ABC中，∠BAC+∠B=π-∠C
∴sinC=sin（∠BAC+∠B）=sin∠BACcosB+cos∠BAC+sinB
=

4

5

×

2

2

+

3

5

×

2

2

=

7 2

10

．

点评：本题在△ABC中给出角B的大小与角A一半的正弦值，求另外角的三角函数值，着重考查了三角形内角和定理、诱导公式、同角三角函数的基本关系和两角和的三角函数公式等知识，属于中档题．