题目内容
已知点P在椭圆
+
=1上，且点P不在x轴上，A，B为椭圆的左、右顶点，直线PA与y轴交于点C，直线BC，PB的斜率分别为kBC，kPB，则kBC2+kPB2的最小值为 ．
| x2 |
| 9 |
| y2 |
| 5 |
考点：椭圆的简单性质
专题：圆锥曲线中的最值与范围问题
分析：首先设直线PA的斜率为k，写出直线方程，然后与椭圆方程联立组成方程组，得到点P的坐标，利用k 表示直线BC和PB的斜率，然后由具体解析式求最小值．
解答：
解：由题意，得A（-3，0），直线PA的斜率存在设为k，则PA 的方程为y=k（x+3），则直线BC斜率为-k，设P（x1，y1），
直线PA与椭圆联立构成方程组得
，得（5+9k2）x2+54k2x+81k2-45=0，
∴x1x2=-3x1=
，
x1=
，y1=k(x1+3)=
，
∴kPB=
=
=-
，
∴kBC2+kPB2=k2+
≥2
=
，当且仅当k2=
时，等号成立，
∴kBC2+kPB2的最小值为
．
直线PA与椭圆联立构成方程组得
|
∴x1x2=-3x1=
| 81k2-45 |
| 5+9k2 |
x1=
| -27k2+15 |
| 5+9k2 |
| 30k |
| 5+9k2 |
∴kPB=
| y1 |
| x1-3 |
| ||
|
| 5 |
| 9k |
∴kBC2+kPB2=k2+
| 25 |
| 81k2 |
k2•
|
| 10 |
| 9 |
| 25 |
| 81k2 |
∴kBC2+kPB2的最小值为
| 10 |
| 9 |
点评：本题考查了椭圆的性质以及椭圆与直线联立方程组，利用根与系数的关系求斜率和的最小值，利用了基本不等式，属于难题．
练习册系列答案
相关题目
在长方体OABC-O1A1B1C1中，|OA|=2，|AB|=3，|AA1|=2，E是BC的中点，建立空间直角坐标系，用向量方法解决下列问题．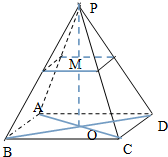
如图，已知四棱锥P-ABCD的底边长与侧棱的长度都是4，ABCD是正方形．