题目内容
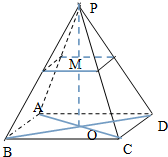 如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形.
如图,已知四棱锥P-ABCD的底边长与侧棱的长度都是4,ABCD是正方形.(1)求该四棱锥的高,表面积;
(2)若M为棱锥的高PO的中点,过点M作平行于棱锥底面的截面,求截得的棱台的体积.
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:(1)判断OP⊥底面ABCD,利用Rt△PED中,DE=2,PD=4,得出PE=2
,再Rt△PEO中OE=2,求解高即可.
(2)求解VP-ABCD=
×42×2
=
,根据体积之比为棱长相似比的关系求解即可得出上半部分V0=
VP-ABCD=
.
| 3 |
(2)求解VP-ABCD=
| 1 |
| 3 |
| 2 |
32
| ||
| 3 |
| 1 |
| 8 |
4
| ||
| 3 |
解答:
 解:(1)∵取CD中点E,连接PE,O为正方形.
解:(1)∵取CD中点E,连接PE,O为正方形.
∵四棱锥P-ABCD的底边长与侧棱的长度都是4,O是正方形ABCD的中心.
∴OP⊥底面ABCD,
∴Rt△PED中,DE=2,PD=4,
∴PE=2
,
∵Rt△PEO中OE=2,
∴PO=
=2
,
∴该四棱锥的高2
,
表面积=42+4×
×4×2
=16+32
(2)VP-ABCD=
×42×2
=
,
∵M为棱锥的高PO的中点,过点M作平行于棱锥底面的截面,
∴上半部分V0=
VP-ABCD=
,
∴截得的棱台的体积=
-
=
 解:(1)∵取CD中点E,连接PE,O为正方形.
解:(1)∵取CD中点E,连接PE,O为正方形.∵四棱锥P-ABCD的底边长与侧棱的长度都是4,O是正方形ABCD的中心.
∴OP⊥底面ABCD,
∴Rt△PED中,DE=2,PD=4,
∴PE=2
| 3 |
∵Rt△PEO中OE=2,
∴PO=
| 12-4 |
| 2 |
∴该四棱锥的高2
| 2 |
表面积=42+4×
| 1 |
| 2 |
| 3 |
| 3 |
(2)VP-ABCD=
| 1 |
| 3 |
| 2 |
32
| ||
| 3 |
∵M为棱锥的高PO的中点,过点M作平行于棱锥底面的截面,
∴上半部分V0=
| 1 |
| 8 |
4
| ||
| 3 |
∴截得的棱台的体积=
32
| ||
| 3 |
4
| ||
| 3 |
28
| ||
| 3 |
点评:本题考查了空间几何体的体积,面积的求解,关键是确定高,斜高,利用直角三角形求解,难度不大,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 执行如图的程序框图,如果输入x,y∈R,那么输出的S的最大值为
执行如图的程序框图,如果输入x,y∈R,那么输出的S的最大值为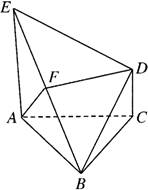 已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;
已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;