题目内容
为了落实大学生村官下乡建设社会主义新农村政策,将5名大学生村官分配到某个镇的3个村就职,每镇至少1名,最多2名,则不同的分配方案有 种.
考点:排列、组合的实际应用
专题:概率与统计,排列组合
分析:根据题意,分2步进行分析:①、先将5名大学生村官分成3组,由分组公式进行计算即可,②、将分好的三组全排列,对应3个村;由分步计数原理计算可得答案.
解答:
解:根据题意,分2步进行分析:
①、先将5名大学生村官分成3组,又由每镇至少1名,最多2名,则必须分成1、2、2的三组,
有
=15种分组方法,
②、将分好的三组全排列,对应3个村,有A33=6种情况,
则共有15×6=90种不同的分配方案;
故答案为90.
①、先将5名大学生村官分成3组,又由每镇至少1名,最多2名,则必须分成1、2、2的三组,
有
| ||||||
|
②、将分好的三组全排列,对应3个村,有A33=6种情况,
则共有15×6=90种不同的分配方案;
故答案为90.
点评:本题考查排列、组合的应用,对于本题要注意“每镇至少1名,最多2名”的限制条件.

练习册系列答案
相关题目
如图所示,程序框图的输出结果是( )


| A、13 | B、14 | C、16 | D、15 |
数列{an}的通项公式为an=(
)2n-4-(
)n-2,则数列{an}( )
| 4 |
| 5 |
| 4 |
| 5 |
| A、有最大项,无最小项 |
| B、有最小项,无最大项 |
| C、既有最大项又有最小项 |
| D、既无最大项又无最小项 |

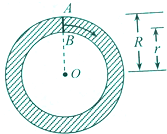 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π× 如图矩形ABCD,AB=4,AD=3,
如图矩形ABCD,AB=4,AD=3,