题目内容
函数f（x）=sin（ωx+
）（ω＞0）的图象与x轴的交点的横坐标构成一个公差为
的等差数列，要得到函数g（x）=sinωx的图象，只需将f（x）的图象（ ）
| π |
| 6 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由条件利用函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答：
解：由题意可得函数的周期为2×
=π=
，∴ω=2．
再根据f（x）=sin（2x+
）=sin2（x+
），
可得将f（x）的图象向右平移
个单位，即可得到函数g（x）=sinωx的图象，
故选：D．
| π |
| 2 |
| 2π |
| ω |
再根据f（x）=sin（2x+
| π |
| 6 |
| π |
| 12 |
可得将f（x）的图象向右平移
| π |
| 12 |
故选：D．
点评：本题主要考查函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如图矩形ABCD，AB=4，AD=3，若实数x，y满足
，则z=
的最小值为（ ）
|
| y+2 |
| x |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
数列{an}的通项公式为an=（
）2n-4-（
）n-2，则数列{an}（ ）
| 4 |
| 5 |
| 4 |
| 5 |
| A、有最大项，无最小项 |
| B、有最小项，无最大项 |
| C、既有最大项又有最小项 |
| D、既无最大项又无最小项 |
已知a为执行如图所示的程序框图输出的结果，又在数列{an}中，a1=1，an+1=2an+a，则（ ）A、an=
| ||||
B、an=2n-2+
| ||||
| C、an=3•2n-1-2 | ||||
| D、an=-2n+3 |
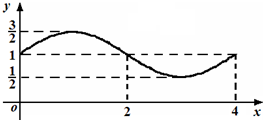
函数f（x）=Asin（ωx+ϕ）+b的图象如图所示，则S=f（0）+f（1）+…+f（2014）等于（ ）
| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知
=i（a，b∈R），其中i为虚数单位，则a2+b2=（ ）
| a+i |
| b+i |
| A、2 | B、3 | C、4 | D、5 |