题目内容
6.若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m( )| A. | 与a有关,且与b有关 | B. | 与a有关,但与b无关 | ||
| C. | 与a无关,且与b无关 | D. | 与a无关,但与b有关 |
分析 结合二次函数的图象和性质,分类讨论不同情况下M-m的取值与a,b的关系,综合可得答案.
解答 解:函数f(x)=x2+ax+b的图象是开口朝上且以直线x=-$\frac{a}{2}$为对称轴的抛物线,
①当-$\frac{a}{2}$>1或-$\frac{a}{2}$<0,即a<-2,或a>0时,
函数f(x)在区间[0,1]上单调,
此时M-m=|f(1)-f(0)|=|a+1|,
故M-m的值与a有关,与b无关
②当$\frac{1}{2}$≤-$\frac{a}{2}$≤1,即-2≤a≤-1时,
函数f(x)在区间[0,-$\frac{a}{2}$]上递减,在[-$\frac{a}{2}$,1]上递增,
且f(0)>f(1),
此时M-m=f(0)-f(-$\frac{a}{2}$)=$\frac{{a}^{2}}{4}$,
故M-m的值与a有关,与b无关
③当0≤-$\frac{a}{2}$<$\frac{1}{2}$,即-1<a≤0时,
函数f(x)在区间[0,-$\frac{a}{2}$]上递减,在[-$\frac{a}{2}$,1]上递增,
且f(0)<f(1),
此时M-m=f(1)-f(-$\frac{a}{2}$)=1+a+$\frac{{a}^{2}}{4}$,
故M-m的值与a有关,与b无关
综上可得:M-m的值与a有关,与b无关
故选:B
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14. 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )| A. | 3,5 | B. | 5,5 | C. | 3,7 | D. | 5,7 |
18.已知函数f(x)=lnx+ln(2-x),则( )
| A. | f(x)在(0,2)单调递增 | B. | f(x)在(0,2)单调递减 | ||
| C. | y=f(x)的图象关于直线x=1对称 | D. | y=f(x)的图象关于点(1,0)对称 |
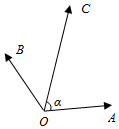 如图,在同一个平面内,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为1,1,$\sqrt{2}$,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α,且tanα=7,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m+n=3.
如图,在同一个平面内,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为1,1,$\sqrt{2}$,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α,且tanα=7,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m+n=3.