题目内容
17.已知函数f(x)=cos$\frac{x}{2}$sin($\frac{x}{2}$+$\frac{π}{3}$)-$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{\sqrt{3}}{4}$.(Ⅰ)求f(x)在区间[0,π]内的单调区间;
(Ⅱ)若f(x0)=$\frac{2}{5}$,x0∈[0,$\frac{π}{2}$],求sinx0的值.
分析 (Ⅰ)求f(x)在区间[0,π]内的单调区间;
(Ⅱ)利用同角三角函数基本关系式以及两角和与差的三角函数化简求解即可.
解答 解:(Ⅰ)函数f(x)=cos$\frac{x}{2}$sin($\frac{x}{2}$+$\frac{π}{3}$)-$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{\sqrt{3}}{4}$
=cos$\frac{x}{2}$($\frac{1}{2}$sin$\frac{x}{2}$+$\frac{\sqrt{3}}{2}$cos$\frac{x}{2}$)-$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{\sqrt{3}}{4}$
=$\frac{1}{4}$sinx-$\frac{\sqrt{3}}{2}•\frac{1+cosx}{2}+\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sin(x-$\frac{π}{3}$).
x∈[0,π],x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
令t=x-$\frac{π}{3}$,y=sint在[-$\frac{π}{3}$,$\frac{π}{2}$]内的单调增函数;
y=sint在$[\frac{π}{2},\frac{2π}{3}]$上单调减函数,
∴f(x)的单调增区间是[0,$\frac{5π}{6}$],单调减区间是[$\frac{5π}{6}$,π].
(Ⅱ)f(x0)=$\frac{2}{5}$,x0∈[0,$\frac{π}{2}$],f(x0)=$\frac{1}{2}$sin(x0-$\frac{π}{3}$)=$\frac{2}{5}$,
可得sin(x0-$\frac{π}{3}$)=$\frac{4}{5}$,cos(x0-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}({x}_{0}-\frac{π}{3})}$=$\frac{3}{5}$,
sinx0=sin[(x0-$\frac{π}{3}$)+$\frac{π}{3}$]=$\frac{1}{2}$×$\frac{4}{5}$$+\frac{\sqrt{3}}{2}×\frac{3}{5}$=$\frac{4+3\sqrt{3}}{10}$.
点评 本题考查三角函数的化简求值,两角和与差的三角函数,正弦函数的单调区间的求法,考查计算能力.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{29}{2}$ | B. | 2$\sqrt{60}$ | C. | $\frac{29}{4}$ | D. | $\frac{102}{7}$ |
| A. | $\frac{5}{16}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{16}$ | D. | $\frac{7}{16}$ |
| A. | -2i | B. | 2i | C. | -2 | D. | 2 |
| A. | 与a有关,且与b有关 | B. | 与a有关,但与b无关 | ||
| C. | 与a无关,且与b无关 | D. | 与a无关,但与b有关 |
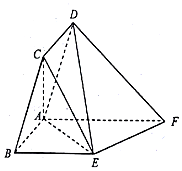 如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.