题目内容
18.已知函数f(x)=lnx+ln(2-x),则( )| A. | f(x)在(0,2)单调递增 | B. | f(x)在(0,2)单调递减 | ||
| C. | y=f(x)的图象关于直线x=1对称 | D. | y=f(x)的图象关于点(1,0)对称 |
分析 由已知中函数f(x)=lnx+ln(2-x),可得f(x)=f(2-x),进而可得函数图象的对称性.
解答 解:∵函数f(x)=lnx+ln(2-x),
∴f(2-x)=ln(2-x)+lnx,
即f(x)=f(2-x),
即y=f(x)的图象关于直线x=1对称,
故选:C.
点评 本题考查的知识点是函数的图象与图象变化,熟练掌握函数图象的对称性是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知i是虚数单位,若复数z满足zi=1+i,则z2=( )
| A. | -2i | B. | 2i | C. | -2 | D. | 2 |
6.若函数f(x)=x2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m( )
| A. | 与a有关,且与b有关 | B. | 与a有关,但与b无关 | ||
| C. | 与a无关,且与b无关 | D. | 与a无关,但与b有关 |
13.已知集合A={x|x<2},B={x|3-2x>0},则( )
| A. | A∩B={x|x<$\frac{3}{2}$} | B. | A∩B=∅ | C. | A∪B={x|x<$\frac{3}{2}$} | D. | AUB=R |
8.下面是关于复数z=2-i的四个命题:p1:|z|=5;p2:z2=3-4i;p3:z的共轭复数为-2+i;p4:z的虚部为-1,其中真命题为( )
| A. | p2,p3 | B. | p1,p2 | C. | p2,p4 | D. | p3,p4 |
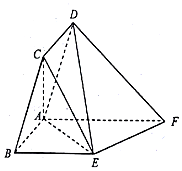 如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠ABC=60°,在直角梯形ABEF中,BE=2,AF=3,BE∥AF,∠BAF=90°,平面ABCD⊥平面ABEF.