题目内容
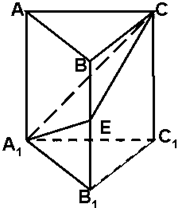如图，在正三棱柱ABC-A1B1C1中，E为BB1的中点，求证：截面A1EC⊥侧面AC1．考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：作EG⊥A1C于G，则G是A1C的中点，连结EA，EC1，则EG⊥AC1，证明EG⊥平面ACC1A1，即可证明截面A1EC⊥侧面AC1．
解答：
证明：作EG⊥A1C于G
∵E是BB1的中点，且A1B1=BC
∴EA1=EC
∴G是A1C的中点
连结AC1，则G是AC1的中点，连结EA，EC1，则EG⊥AC1
又∵A1C∩AC1=G，
∴EG⊥平面ACC1A1，EG?截面A1EC
∴截面A1EC⊥平面ACC1A1．
证明：作EG⊥A1C于G ∵E是BB1的中点，且A1B1=BC
∴EA1=EC
∴G是A1C的中点
连结AC1，则G是AC1的中点，连结EA，EC1，则EG⊥AC1
又∵A1C∩AC1=G，
∴EG⊥平面ACC1A1，EG?截面A1EC
∴截面A1EC⊥平面ACC1A1．
点评：本小题考查空间线面关系，正三棱柱的性质，逻辑思维能力，空间想象能力及运算能力．
练习册系列答案
智能训练练测考系列答案
相关题目
设a，b是方程x2-x•cosθ+sinθ=0的两个不相等的实数根，那么过两点A（a，a2），B（b，b2）的直线与圆x2+y2=1的位置关系是（ ）
| A、相切 | B、相交或相切 |
| C、相离 | D、相切或相离 |
设随机变量ξ～N（1，σ2），若P（0＜ξ＜1）=0.3，则P（ξ＜2）=（ ）
| A、0.2 | B、0.7 |
| C、0.8 | D、0.5 |
已知在棱长为1的正方体ABCD-A1B1C1D1中，E、F、M分别是A1C1，A1D和B1A上任一点，求证：平面A1EF∥平面B1MC．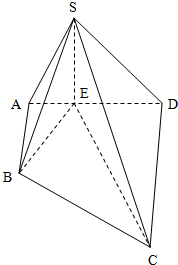
如图，在四棱锥S-ABCD中，AB∥CD，∠BAD=90°，平面SAD⊥平面ABCD，SE⊥AD于点E，CD=DE=2AB=2AE，
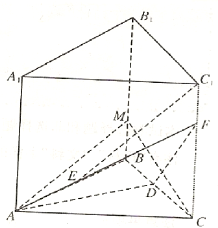如图，在直三棱柱ABC-A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB=AC，AA1=3，BC=CF=2