题目内容
设a,b是方程x2-x•cosθ+sinθ=0的两个不相等的实数根,那么过两点A(a,a2),B(b,b2)的直线与圆x2+y2=1的位置关系是( )
| A、相切 | B、相交或相切 |
| C、相离 | D、相切或相离 |
考点:直线与圆的位置关系
专题:直线与圆
分析:由a,b为已知方程的两个不相等的实数根,得到根的判别式大于0表示出a+b与ab,表示出直线AB解析式,利用点到直线的距离公式表示出圆心到直线的距离d,比较d与r的大小即可做出判断.
解答:
解:∵a,b是方程x2-x•cosθ+sinθ=0的两个不相等的实数根,
∴a+b=cosθ,ab=sinθ,
由圆的方程得到圆心(0,0),半径r=1,
过两点A(a,a2),B(b,b2)的直线方程为y-a2=
(x-a),
整理得:(a+b)x-y-ab=0,即cosθx-y-sinθ=0,
∵圆心(0,0)到直线的距离d=
≤1,
∴直线与圆的位置关系是相交或相切.
故选:B.
∴a+b=cosθ,ab=sinθ,
由圆的方程得到圆心(0,0),半径r=1,
过两点A(a,a2),B(b,b2)的直线方程为y-a2=
| a2-b2 |
| a-b |
整理得:(a+b)x-y-ab=0,即cosθx-y-sinθ=0,
∵圆心(0,0)到直线的距离d=
| |sinθ| | ||
|
∴直线与圆的位置关系是相交或相切.
故选:B.
点评:此题考查了直线与圆的位置关系,涉及的知识有:韦达定理,点到直线的距离公式,以及直线的两点式方程,弄清题意是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
因为指数函数y=ax(a>0且a≠1)是增函数,而y=(
)x是指数函数,所以y=(
)x是增函数,以上推理错误的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提 | B、小前提 |
| C、推理形式 | D、以上都错 |
已知全集U={-1,0,1,3},N={0,1,3},则∁UN=( )
| A、{3} | B、{0,1} |
| C、{-1} | D、{-1,3} |
某几何体的三视图及其尺寸如图所示,则该几何体的表面积是( )
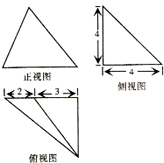

A、30+6
| ||
B、28+6
| ||
C、56+12
| ||
D、60+12
|
已知向量
=(3,4),
=(-1,2),则
=( )
| AB |
| AC |
| CB |
| A、(4,2) |
| B、(2,6) |
| C、(5,3) |
| D、(-1,5) |
已知sinα>0,cosα>0,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
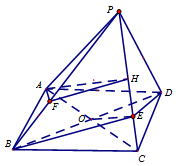 四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,
四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,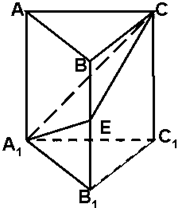 如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.
如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.