题目内容
已知圆C:(x+3)2+(y-6)2=36,直线l过点M(0,3)把圆C分成两部分,且使得这两部分面积之差的绝对值最大.
(Ⅰ)求直线l的方程;
(Ⅱ)设直线l与圆C交于点A、B,点P是圆C上异于A、B的一点,求△PAB面积的最大值.
(Ⅰ)求直线l的方程;
(Ⅱ)设直线l与圆C交于点A、B,点P是圆C上异于A、B的一点,求△PAB面积的最大值.
考点:直线和圆的方程的应用,圆的标准方程
专题:综合题,直线与圆
分析:(Ⅰ)由题意得到当直线l与圆相交的弦最短时,把圆分成的两部分面积之差的绝对值最大,求出MC所在直线方程的斜率,即可求直线l的方程;
(Ⅱ)求出圆心到直线AB的距离以及弦长AB,根据圆的性质可得点P到AB距离的最大值,即可求出△PAB面积的最大值.
(Ⅱ)求出圆心到直线AB的距离以及弦长AB,根据圆的性质可得点P到AB距离的最大值,即可求出△PAB面积的最大值.
解答:
解:(Ⅰ)由题意得M(0,3)在圆内,
当直线l与圆相交的弦最短时,把圆分成的两部分面积之差的绝对值最大,此时MC⊥l.
又直线MC的斜率为
=-1,∴kl=1,
∴直线l的方程为x-y+3=0.(6分)
(Ⅱ)圆心C到直线l的距离为
=3
,∴|AB|=2
=6
,
根据圆的性质可得点P到AB距离的最大值为3
+6,
∴△PAB面积的最大值为:
×6
×(3
+6)=18+18
.(12分)
当直线l与圆相交的弦最短时,把圆分成的两部分面积之差的绝对值最大,此时MC⊥l.
又直线MC的斜率为
| 6-3 |
| -3-0 |
∴直线l的方程为x-y+3=0.(6分)
(Ⅱ)圆心C到直线l的距离为
| |-3-6+3| | ||
|
| 2 |
| 36-18 |
| 2 |
根据圆的性质可得点P到AB距离的最大值为3
| 2 |
∴△PAB面积的最大值为:
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:此题考查了直线与圆的位置关系,考查圆的切线性质,两直线垂直的性质,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知全集U={-1,0,1,3},N={0,1,3},则∁UN=( )
| A、{3} | B、{0,1} |
| C、{-1} | D、{-1,3} |
命题“对任意x∈R,总有x2+1>0”的否定是( )
| A、“对任意x∉R,总有x2+1>0” |
| B、“对任意x∈R,总有x2+1≤0” |
| C、“存在x∈R,使得x2+1>0” |
| D、“存在x∈R,使得x2+1≤0” |
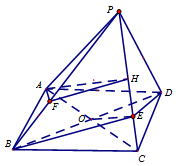 四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,
四棱锥P-ABCD中,底面ABCD是平行四边形,E∈PC,F∈PB,
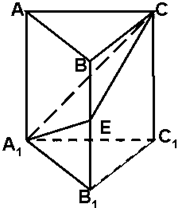 如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.
如图,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1EC⊥侧面AC1.