题目内容
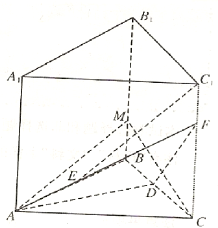如图，在直三棱柱ABC-A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB=AC，AA1=3，BC=CF=2（1）求证：C1E∥平面ADF；
（2）若点M在棱BB1上且BM=1，求证：平面ACM⊥平面ADF．
考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：（1）连接AD、CE并相交于O点，连接OF，则OF为平面CEC1与平面ADF的相交线，由已知条件推导出OF∥C1E，由此能证明C1E∥平面ADF．
（2）平面BCC1B1∩平面ADF=DF，平面BCC1B1∩平面ACM=CM，由已知条件推志导△CBM≌△FCD，从而得到DF⊥CM，由此能证明平面ACM⊥平面ADF．
（2）平面BCC1B1∩平面ADF=DF，平面BCC1B1∩平面ACM=CM，由已知条件推志导△CBM≌△FCD，从而得到DF⊥CM，由此能证明平面ACM⊥平面ADF．
解答：
（1）证明：连接AD、CE并相交于O点，
连接OF，则OF为平面CEC1与平面ADF的相交线，
在△ABC中，D、E分别是BC、AB的中点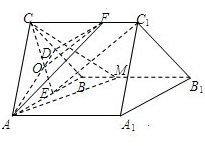
则O点为△ABC的重心，即 OC=2OE
=
，
又CC1=AA1=3，CF=2，
=
，
在△ECC1、△COF中，
=
，
∴OF∥C1E，
∵OF?平面ADF，C1E不包含于平面ADF，
∴C1E∥平面ADF．
（2）∵平面BCC1B1∩平面ADF=DF，
平面BCC1B1∩平面ACM=CM，
∵BC=CF=2，D是棱BC的中点，BM=1，
∠CBM=∠FCD=90°，
∴△CBM≌△FCD，∴∠BCM=∠CFD，
∴DF⊥CM，
∴平面ACM⊥平面ADF．
连接OF，则OF为平面CEC1与平面ADF的相交线，
在△ABC中，D、E分别是BC、AB的中点
则O点为△ABC的重心，即 OC=2OE
| OC |
| CE |
| 3 |
| 2 |
又CC1=AA1=3，CF=2，
| CF |
| CC1 |
| 2 |
| 3 |
在△ECC1、△COF中，
| CF |
| CC1 |
| OC |
| CE |
∴OF∥C1E，
∵OF?平面ADF，C1E不包含于平面ADF，
∴C1E∥平面ADF．
（2）∵平面BCC1B1∩平面ADF=DF，
平面BCC1B1∩平面ACM=CM，
∵BC=CF=2，D是棱BC的中点，BM=1，
∠CBM=∠FCD=90°，
∴△CBM≌△FCD，∴∠BCM=∠CFD，
∴DF⊥CM，
∴平面ACM⊥平面ADF．
点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
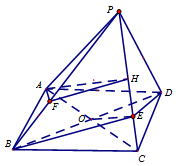四棱锥P-ABCD中，底面ABCD是平行四边形，E∈PC，F∈PB，
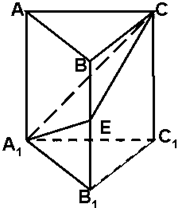如图，在正三棱柱ABC-A1B1C1中，E为BB1的中点，求证：截面A1EC⊥侧面AC1．
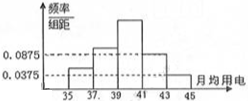某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如图．其中直方图从左到右前3个小矩形的面积之比为1：2：3．