Question

5．如图，长方体ABCD-A₁B₁C₁D₁中，AB=16，AD=10，AA₁=6，点P在棱C₁D₁上，且D₁P=6．
（1）求三棱锥P-A₁CD的体积；
（2）请作图：经过点P在上底面内画一条直线和PB垂直；
（3）请作图：经过点P作长方体的一个截面，且截面图形为正方形．（注意：要求写出作法，明确所作直线与棱的交点的位置，不需要给出证明过程）

Answer 1

分析 （1）过D₁作D₁M⊥A₁D，则D₁M⊥平面A₁DC，所以D₁M等于棱锥的高，
（2）连结PB，PB₁，在上底面过P作PN⊥PB₁，则直线PN就是所要求的直线．
（3）在A₁B₁上取点E，使得A₁E=D₁P=6．在AB上取点F，在CD上取点G，使得BF=CG=2，连结PE，EF，FG，PG，则截面PEFG为所要求的截面．

解答 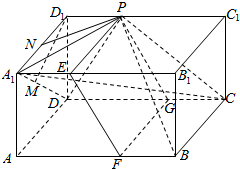（1）过D₁作D₁M⊥A₁D，则D₁M⊥平面A₁DC，A₁D=$\sqrt{{A}_{1}{A}^{2}+A{D}^{2}}$=$\sqrt{136}$．
∵A₁D₁•D₁D=A₁D•D₁M，∴D₁M=$\frac{{A}_{1}{D}_{1}•{D}_{1}D}{{A}_{1}D}$=$\frac{30}{\sqrt{34}}$．
∴V${\;}_{棱锥P-{A}_{1}CD}$=$\frac{1}{3}$•S${\;}_{△{A}_{1}CD}$•D₁M=$\frac{1}{3}×\frac{1}{2}×{A}_{1}D×DC×{D}_{1}M$=$\frac{1}{3}×\frac{1}{2}×\sqrt{136}×16×\frac{30}{\sqrt{34}}$=160．
（2）连结PB，PB₁，在上底面过P作PN⊥PB₁，则直线PN就是所要求的直线．
（3）在A₁B₁上取点E，使得A₁E=D₁P=6．在AB上取点F，在CD上取点G，使得BF=CG=2，
连结PE，EF，FG，PG，则截面PEFG为所要求的截面．

点评 本题考查了棱柱的结构特征，线面垂直的性质与判定，棱锥的体积计算，属于中档题．