��Ŀ����
13����ֱ������ϵxOy����ԲC1��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2������F2Ҳ��������C2��y2=4x�Ľ��㣬��MΪC1��C2�ڵ�һ���Ľ��㣬��|MF2|=$\frac{5}{3}$��1������ԲC1�ķ��̣�
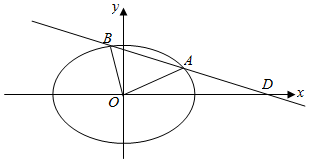
��2��������D��4��0����ֱ��l��C1���ڲ�ͬ������A��B����A��DB֮�䣬�����AOD���BOD�����ֵ��ȡֵ��Χ��
���� ��1�����M�����꣬������Բ�����з�����ó�a��b��
��2����l���̣�x=my+4�����������飬���ø���ϵ���Ĺ�ϵ�ó�A��B������Ĺ�ϵ�����=$\frac{{S}_{��AOD}}{{S}_{��BOD}}$=$\frac{{y}_{1}}{{y}_{2}}$����y1=y2�ˣ��������ϵ���Ĺ�ϵ�ó�m2���ڦ˵ĺ���������m2�ķ�Χ���ɵó��˵ķ�Χ��
���  �⣺��1��������֪F2��1��0������F1��-1��0����
�⣺��1��������֪F2��1��0������F1��-1��0����
��M��x1��y1������|MF2|=x1+1=$\frac{5}{3}$����x1=$\frac{2}{3}$��
��y1=2$\sqrt{{x}_{1}}$=$\frac{2\sqrt{6}}{3}$����M��$\frac{2}{3}$��$\frac{2\sqrt{6}}{3}$����
��$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}=1}\\{\frac{��\frac{2}{3}��^{2}}{{a}^{2}}+\frac{��\frac{2\sqrt{6}}{3}��^{2}}{{b}^{2}}=1}\end{array}\right.$�����a2=4��b2=3��???
����ԲC1�ķ���Ϊ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1��
��2��������ֱ֪��l��б�ʴ����Ҳ�Ϊ0����l�ķ���Ϊx=my+4��
����������$\left\{\begin{array}{l}{x=my+4}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���������3m2+4��y2+24my+36=0��
���=576m2-144��3m2+4����0�����m2��4��
��A��x1��y1����B��x2��y2����
��y1+y2=-$\frac{24m}{3{m}^{2}+4}$��y1y2=$\frac{36}{3{m}^{2}+4}$��
���=$\frac{{S}_{��AOD}}{{S}_{��BOD}}$=$\frac{{y}_{1}}{{y}_{2}}$����y1=y2�ˣ���0���ˣ�1��
��y1=y2�˴���y1+y2=-$\frac{24m}{3{m}^{2}+4}$��y1y2=$\frac{36}{3{m}^{2}+4}$�ɵã�
$\left\{\begin{array}{l}{����+1��{y}_{2}=-\frac{24m}{3{m}^{2}+4}}\\{{��{y}_{2}}^{2}=\frac{36}{3{m}^{2}+4}}\end{array}\right.$����ȥy2��$\frac{����+1��^{2}}{��}$=$\frac{16{m}^{2}}{3{m}^{2}+4}$��
��m2=$\frac{4����+1��^{2}}{10��-3{��}^{2}-3}$��
��$\frac{4����+1��^{2}}{10��-3{��}^{2}-3}$��4�����$\frac{1}{3}���ˣ�1$��1���ˣ�3���ᣩ��
���AOD���BOD�����ֵ��ȡֵ��Χ�ǣ�$\frac{1}{3}$��1����
���� ���⿼������Բ�����ʣ�ֱ������Բ��λ�ù�ϵ�������е��⣮

| A�� | 4 | B�� | 6 | C�� | 8 | D�� | 10 |
| A�� | y=-3x+5 | B�� | y=3x-1 | C�� | y=3x+5 | D�� | y=2x |
| A�� | $A_{100-n}^{80}$ | B�� | $A_{100-n}^{20-n}$ | C�� | $A_{100-n}^{81}$ | D�� | $A_{20-n}^{81}$ |
| ��� | ���� | ��̸���� | Ը��ʹ�� |
| 1 | [18��28�� | 4 | 4 |
| 2 | [28��38�� | 9 | 9 |
| 3 | [38��48�� | 16 | 15 |
| 4 | [48��58�� | 15 | 12 |
| 5 | [58��68�� | 6 | 2 |
�������ӵ�5��ı������߷�̸�������ѡȡ2�˽����ٵ��飬��2����������1��Ը��ѡ��˿���������ײ͵ĸ��ʣ�
��������ͳ��������д����2��2�����������ж���48��Ϊ�ֽ�㣬�ܷ��ڷ�������1%��ǰ������Ϊ���Ƿ�Ը��ѡ��˿���������ײ����˵������йأ�
| ���䲻����48������� | �������48������� | �ϼ� | |
| Ը��ʹ�õ����� | |||
| ��Ը��ʹ�õ����� | |||
| �ϼ� |
| P��k2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A�� | 12��cm2 | B�� | 6 cm2 | C�� | 6��cm2 | D�� | 4 cm2 |